
| A. | ∠D=40°,∠E=80°,∠A=60°,∠B=80° | |
| B. | ∠A=∠D,AB:AC=DF:EF | |
| C. | ∠B=∠E=90°,BC:EF=AC:DF | |
| D. | AB=1,BC=2,CA=1.5,DE=6,EF=4,FD=8 |
分析 由两角分别相等的两个三角形相似得出A能判定△ABC∽△DEF;
两边成比例,但是夹角不相等,得出B不能判定△ABC∽△DEF;
由直角三角形相似的判定方法得出C能判定△ABC∽△DEF;
由三边成比例的两个三角形相似得出D能判定△ABC∽△DEF;即可得出结论.
解答 解:A能判定△ABC∽△DEF;理由:
∵∠C=180°-∠A-∠B=180°-60°-80°=40°,
∴∠C=∠D,
又∵∠B=∠E=80°,
∴△ABC∽△FED;
B不能判定△ABC∽△DEF;理由:
∵AB:AC=DF:EF,∠A=∠D,而不是∠A=∠F,
∴不能判定△ABC∽△DEF;
C能判定△ABC∽△DEF;理由:
∵∠B=∠E=90°,
∴AC、DF分别为斜边,
∵BC:EF=AC:DF,
∴△ABC∽△DEF;
D能判定△ABC∽△DEF;理由:
∵$\frac{AB}{EF}=\frac{1}{4}$,$\frac{BC}{FD}=\frac{2}{8}=\frac{1}{4}$,$\frac{CA}{DE}=\frac{1.5}{6}=\frac{1}{4}$,
∴$\frac{AB}{EF}=\frac{BC}{FD}=\frac{CA}{DE}$,
∴△ABC∽△EFD.
故选:B.
点评 本题考查了相似三角形的判定方法、三角形内角和定理;熟练掌握相似三角形的判定方法,并能进行推理论证与计算是解决问题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:填空题
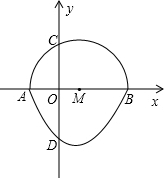 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),C的坐标为(0,$\sqrt{3}$).则经过点D的“蛋圆”切线的解析式是y=-2x-3.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),C的坐标为(0,$\sqrt{3}$).则经过点D的“蛋圆”切线的解析式是y=-2x-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.
已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
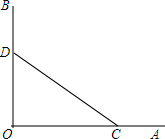 画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.
画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=4,b=-3 | B. | a=2,b=-1 | C. | a=-1,b=1 | D. | a=-1,b=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com