
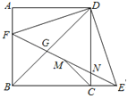
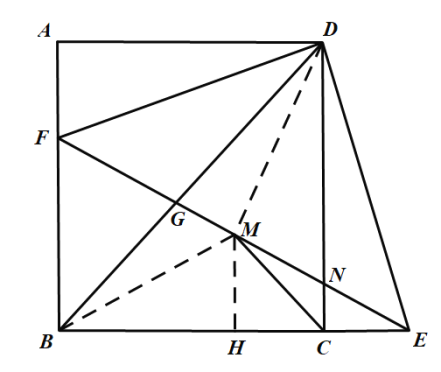
【题目】如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连结EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DE=DF;②∠CME=∠CDE;③DG2=GN GE;④若BF=2,![]() 则正确的结论有( )个.
则正确的结论有( )个.
A.4B.3C.2D.1
【答案】A
【解析】
①根据正方形的性质可证明![]() ,则可判断①正误;
,则可判断①正误;
②首先利用![]() 和直角三角形斜边中线的性质得出
和直角三角形斜边中线的性质得出![]() ,然后利用三角形外角的性质和直角三角形两锐角互余即可判断;
,然后利用三角形外角的性质和直角三角形两锐角互余即可判断;
③首先证明![]() ,则有
,则有![]() ,即可判断③的正误;
,即可判断③的正误;
④首先利用平行线分线段成比例求出MH的长度,然后解直角三角形即可求出MC的长度,由此可判断④的正误.
∵四边形ABCD是正方形,
∴![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,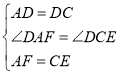
![]() ,
,
![]() ,故①正确;
,故①正确;
连接DM,BM,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
∵点M是EF的中点,
∴![]() .
.
![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,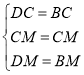
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,故②正确;
,故②正确;
∵![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,故③正确;
,故③正确;
过点M作![]() 交BC于H,
交BC于H,
![]() ,
,
![]() ,
,
∴![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,故④正确;
,故④正确;
∴正确的有:①②③④,
故选:A.


科目:初中数学 来源: 题型:
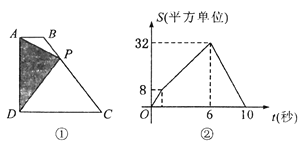
【题目】如图①,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 从
从![]() 点出发,以每秒2个单位长度的速度,按
点出发,以每秒2个单位长度的速度,按![]() 的顺序在边上匀速运动,设
的顺序在边上匀速运动,设![]() 点的运动时间为
点的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,
,![]() 关于
关于![]() 的函数图像如图②所示,当
的函数图像如图②所示,当![]() 运动到
运动到![]() 中点时,
中点时,![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
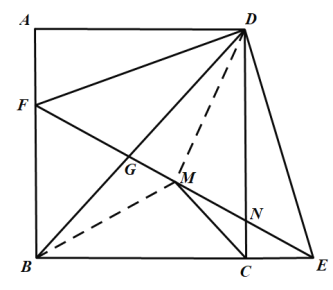
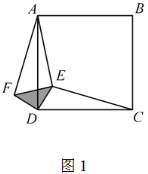
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若![]() ,求∠AED的度数;
,求∠AED的度数;
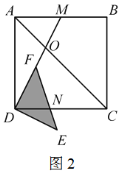
(3)若BC=4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的边DF与边DM重合时(如图2),若![]() ,求DN的长.
,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y=![]() 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB为⊙O的直径,点C,E在⊙O上,![]() ,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F.
,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F.
(1)求证:CF=BF;
(2)若cos∠ABE![]() ,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.
,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线.以
的角平分线.以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() .
.
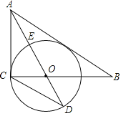
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)已知![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的值.
的值.
(3)在(2)的条件下,设![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
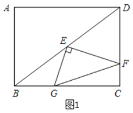
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是对角线BD的中点,直角∠GEF的两直角边EF、EG分别交CD、BC于点F、G.
(1)若点F是边CD的中点,求EG的长;
(2)当直角∠GEF绕直角顶点E旋转,旋转过程中与边CD、BC交于点F、G.∠EFG的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠EFG的值;
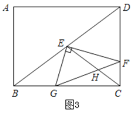
(3)如图3,连接CE交FG于点H,若![]() ,请求出CF的长.
,请求出CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
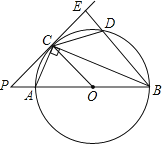
【题目】在Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,点D是![]() 上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
(1)求证:∠PCA=∠PBC;
(2)若PC=8,PA=4,∠ECD=∠PCA,以点C为圆心,半径为5作⊙C,试判断⊙C与直线BD的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com