练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    对如图1所示的图形的三个说法①是半圆；②是弓形；③是扇形，其中正确的个数是

    [　　]

    A．3

    B．2

    C．1

    D．0

    答案：B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    把三角形形状的纸片放在方框纸上，使其每一个顶点都在格点上，如图1所示（方格边长均为1）．对这个三角形进剪切、拼接后，可以得到一个平行四边形，如图2中阴影部分所示．
    剪切、拼接的方案如下：如图2，取BC的中点M，连AM．剪下△AMC后，沿直线BC翻折，所得图形称为△DMC；再把△DMC沿射线CA方向平移线段CA的长度后，可得到平行四边形AEBM．
    我们约定：剪切、拼接 时，纸片的每一部分都要被用到，而且不得用所给纸片以外的纸片．

    （1）请你采用不同于图2的剪切、拼接方案，也得到一个平行四边形，并说明你的剪切、拼接方案，同时在图3中用阴影表示出你得到的平行四边形；
    （2）对这个三角形进行剪切、拼接后，也可以得到一梯形．试在图4中，用阴影表示出你得到的梯形（不必说明剪切、拼接方案，但必须保留作图痕迹）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    意大利文艺复兴时代的著名画家达·芬奇对勾股定理也曾进行了研究．他验证勾股定理的方法可以从下面的实验中得到体现．

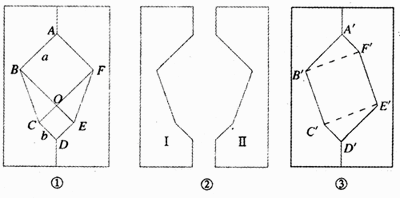
    (1)在一张长方形的纸板上画两个边长分别为a，b的正方形，并连接BC，FE(如图①所示)．

    (2)沿ABCDEFA剪下，得到两个大小相同的纸板Ⅰ，Ⅱ，如图②所示．

    (3)将纸板Ⅱ翻转后与Ⅰ拼成如图③所示的图形．

    (4)比较图①，图③中两个多边形ABCDEF和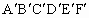的面积，你能验证勾股定理吗？请动手做一做．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    把三角形形状的纸片放在方框纸上，使其每一个顶点都在格点上，如图1所示（方格边长均为1）．对这个三角形进剪切、拼接后，可以得到一个平行四边形，如图2中阴影部分所示．
    剪切、拼接的方案如下：如图2，取BC的中点M，连AM．剪下△AMC后，沿直线BC翻折，所得图形称为△DMC；再把△DMC沿射线CA方向平移线段CA的长度后，可得到平行四边形AEBM．
    我们约定：剪切、拼接 时，纸片的每一部分都要被用到，而且不得用所给纸片以外的纸片．

    （1）请你采用不同于图2的剪切、拼接方案，也得到一个平行四边形，并说明你的剪切、拼接方案，同时在图3中用阴影表示出你得到的平行四边形；
    （2）对这个三角形进行剪切、拼接后，也可以得到一梯形．试在图4中，用阴影表示出你得到的梯形（不必说明剪切、拼接方案，但必须保留作图痕迹）．

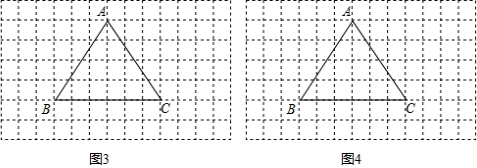
    查看答案和解析>>

    科目：初中数学 来源：2009年安徽省巢湖市庐江县初中毕业班质量检测数学试卷（解析版） 题型：解答题

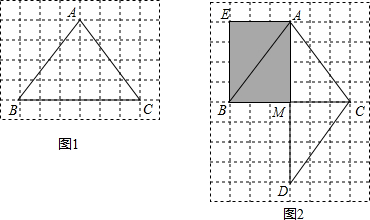
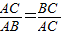    （2009•庐江县模拟）如图1所示，点C将线段AB分成两部分，如果，那么点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果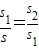，那么称直线l为该图形的黄金分割线．
    （1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点，如图2所示，则直线CD是△ABC的黄金分割线，你认为对吗？说说你的理由；
    （2）请你说明：三角形的中线是否是该三角形的黄金分割线．

    查看答案和解析>>

    同步练习册答案