
”¾ĢāÄæ”泬ŹŠ×¼±ø¹ŗ½ųA”¢BĮ½ÖÖĘ·ÅʵÄŅūĮĻ¹²100¼ž£¬Į½ÖÖŅūĮĻĆ漞ĄūČó·Ö±šŹĒ15ŌŖŗĶ13ŌŖ£®Éč¹ŗ½ųAÖÖŅūĮĻx¼ž£¬ĒŅĖł¹ŗ½ųµÄĮ½ÖÖŅūĮĻÄÜČ«²æĀō³ö£¬»ńµĆµÄ×ÜĄūČóĪŖyŌŖ£®
£Ø1£©ĒóyÓėxµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©øł¾ŻĮ½ÖÖŅūĮĻĄś“ĪĻśĮæ¼ĒŌŲ£ŗAÖÖŅūĮĻÖĮÉŁ¹ŗ½ų30¼ž£¬BÖÖŅūĮĻ¹ŗ½ųŹżĮæ²»ÉŁÓŚAÖÖŅūĮĻ¼žŹżµÄ2±¶£®ĪŹ£ŗA”¢BĮ½ÖÖŅūĮĻ½ų»õ·½°øÓŠ¼øÖÖ£æÄÄŅ»ÖÖ·½°øÄÜŹ¹³¬ŹŠĖł»ńĄūČó×īøߣæ×īøߥūČóŹĒ¶ąÉŁ£æ
”¾“š°ø”æ£Ø1£©y£½2x+1300£»
£Ø2£©¹ŗ½ųAÖÖŅūĮĻ33¼ž£¬BÖÖŅūĮĻ67¼ž£¬³¬ŹŠĖł»ńĄūČó×īøߣ¬×īøߥūČóŹĒ1366ŌŖ
”¾½āĪö”æ
£Ø1£©Éč¹ŗ½ųAÖÖŅūĮĻx¼ž£¬Ōņ¹ŗ½ųBÖÖŅūĮĻ£Ø100©x£©¼ž£¬øł¾ŻĄūČóµČÓŚĆ漞µÄĄūČó”Į¼žŹż¾ĶæÉŅŌµĆ³ö½įĀŪ£»
£Ø2£©øł¾ŻĢāŅāæÉŅŌ±ķŹ¾³ö£ŗAÖÖŅūĮĻÖĮÉŁ¹ŗ½ų30¼ž£¬ĪŖx”Ż30£¬BÖÖŅūĮĻ¹ŗ½ųŹżĮæ²»ÉŁÓŚAÖÖŅūĮĻ¼žŹżµÄ2±¶ĪŖ100©2x”Ż2x£¬ÓÉÕāĮ½øö²»µČŹ½¹¹³É²»µČŹ½×éĒó³öĘä½ā£¬øł¾ŻŅĄ“ĪŗÆŹżµÄŠŌÖŹµĆ³ö“š°ø¼“æÉ£®
£Ø1£©yÓėxŗÆŹż¹ŲĻµŹ½ŹĒ£ŗ
y£½15x+13£Ø100©x£©
£½2x+1300£¬
¼“y£½2x+1300£®
£Ø2£©ÓÉĢāŅā£¬µĆ![]() £¬
£¬
½āµĆ30”Üx”Ü33![]() £¬
£¬
ĖüµÄÕūŹż½āĪŖx£½30£¬31£¬32£¬33£®
”ąA”¢BĮ½ÖÖŅūĮĻ½ų»õ·½°øÓŠ4ÖÖ£¬
”ßyĖę×ÅxµÄŌö“ó¶ųŌö“ó£¬
”ąµ±x£½33Ź±£¬yČ”µĆ×ī“óÖµy£½2”Į33+1300£½1366
¼“·Ö±š¹ŗ½ųAÖÖŅūĮĻ33¼ž£¬BÖÖŅūĮĻ67¼ž£¬³¬ŹŠĖł»ńĄūČó×īøߣ¬×īøߥūČóŹĒ1366ŌŖ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ČēĶ¼1£¬µČŃüÖ±½ĒČż½ĒŠĪABCÖŠ£¬”ĻACB=90”ć£¬CB=CA£¬Ö±ĻßED¾¹żµćC£¬¹żA×÷AD”ĶEDÓŚµćD£¬¹żB×÷BE”ĶEDÓŚµćE£®
ĒóÖ¤£ŗ”÷BEC”Õ”÷CDA£»
£ØÄ£ŠĶÓ¦ÓĆ£©
£Ø2£©¢ŁŅŃÖŖÖ±Ļßl1£ŗy=![]() x+4Óė×ų±źÖį½»ÓŚµćA”¢B£¬½«Ö±Ļßl1ČʵćAÄꏱÕėŠż×Ŗ45oÖĮÖ±Ļßl2£¬ČēĶ¼2£¬ĒóÖ±Ļßl2µÄŗÆŹż±ķ“ļŹ½£»
x+4Óė×ų±źÖį½»ÓŚµćA”¢B£¬½«Ö±Ļßl1ČʵćAÄꏱÕėŠż×Ŗ45oÖĮÖ±Ļßl2£¬ČēĶ¼2£¬ĒóÖ±Ļßl2µÄŗÆŹż±ķ“ļŹ½£»
¢ŚČēĶ¼3£¬³¤·½ŠĪABCO£¬OĪŖ×ų±źŌµć£¬µćBµÄ×ų±źĪŖ£Ø8£¬-6£©£¬µćA”¢C·Ö±šŌŚ×ų±źÖįÉĻ£¬µćPŹĒĻ߶ĪBCÉĻµÄ¶Æµć£¬µćDŹĒÖ±Ļßy=-2x+6ÉĻµÄ¶ÆµćĒŅŌŚµŚĖÄĻóĻŽ£®Čō”÷APDŹĒŅŌµćDĪŖÖ±½Ē¶„µćµÄµČŃüÖ±½ĒČż½ĒŠĪ£¬ĒėÖ±½ÓŠ“³öµćDµÄ×ų±ź£®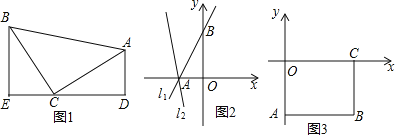
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĄīŹ¦øµøŗŌšŠŽĄķĪŅŠ£æĪץŅĪ£¬ĻÖÖŖµĄĄīŹ¦øµŠŽĄķ2ÕÅæĪץŗĶ3°ŃŅĪ×Ó¹²Šč86·ÖÖÓ£¬ŠŽĄķ5ÕÅæĪץŗĶ2°ŃŅĪ×Ó¹²Šč149·ÖÖÓ£®
£Ø1£©ĒėĪŹĄīŹ¦øµŠŽĄķ1ÕÅæĪץŗĶ1°ŃŅĪ×Óø÷Šč¶ąÉŁ·ÖÖÓ
£Ø2£©ĻÖĪŅŠ£ÓŠ12ÕÅæĪץŗĶ14°ŃŅĪ×ÓŠčŅŖŠŽĄķ£¬ŅŖĒó1Ģģ×öĶź£¬ĄīŹ¦øµĆæĢģ¹¤×÷8Š”Ź±£¬ĒėĪŹĄīŹ¦øµÄÜŌŚÉĻ°ąŹ±¼äÄŚŠŽĶźĀš£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚŹżÖįÉĻÓŠA”¢B”¢C”¢DĖÄøöÕūŹżµć![]() ¼“ø÷µć¾ł±ķŹ¾ÕūŹż
¼“ø÷µć¾ł±ķŹ¾ÕūŹż![]() £¬ĒŅ
£¬ĒŅ![]() £¬ČōA”¢DĮ½µć±ķŹ¾µÄŹżµÄ·Ö±šĪŖ
£¬ČōA”¢DĮ½µć±ķŹ¾µÄŹżµÄ·Ö±šĪŖ![]() ŗĶ6£¬µćEĪŖBDµÄÖŠµć£¬ÄĒĆ“øĆŹżÖįÉĻÉĻŹöĪåøöµćĖł±ķŹ¾µÄÕūŹżÖŠ£¬ĄėĻ߶ĪBDµÄÖŠµć×ī½üµÄÕūŹżŹĒ
ŗĶ6£¬µćEĪŖBDµÄÖŠµć£¬ÄĒĆ“øĆŹżÖįÉĻÉĻŹöĪåøöµćĖł±ķŹ¾µÄÕūŹżÖŠ£¬ĄėĻ߶ĪBDµÄÖŠµć×ī½üµÄÕūŹżŹĒ![]() ””””
””””![]()
![]()
A. ![]() B. 0C. 1D. 2
B. 0C. 1D. 2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øöÓÉČōøÉŠ”Õż·½ŠĪ¶Ń³ÉµÄ¼øŗĪĢ壬Ėü“ÓÕżĆęæ“ŗĶ“Ó×óĆę擵ÄĶ¼ŠĪČēĶ¼1ĖłŹ¾£®
![]() Õāøö¼øŗĪĢåæÉŅŌŹĒĶ¼2ÖŠ¼×£¬ŅŅ£¬±ūÖŠµÄ______£»
Õāøö¼øŗĪĢåæÉŅŌŹĒĶ¼2ÖŠ¼×£¬ŅŅ£¬±ūÖŠµÄ______£»
![]() Õāøö¼øŗĪĢå×ī¶ąÓÉ______øöŠ”Õż·½Ģå¶Ń³É£¬×īÉŁÓÉ______øöŠ”Õż·½Ģå¶Ń³É£»
Õāøö¼øŗĪĢå×ī¶ąÓÉ______øöŠ”Õż·½Ģå¶Ń³É£¬×īÉŁÓÉ______øöŠ”Õż·½Ģå¶Ń³É£»
![]() ĒėŌŚĶ¼3ÖŠÓĆŅõÓ°²æ·Ö»³ö·ūŗĻ×īÉŁĒéæöŹ±µÄŅ»øö“ÓÉĻĆęĶłĻĀæ“µĆµ½µÄĶ¼ŠĪ£®
ĒėŌŚĶ¼3ÖŠÓĆŅõÓ°²æ·Ö»³ö·ūŗĻ×īÉŁĒéæöŹ±µÄŅ»øö“ÓÉĻĆęĶłĻĀæ“µĆµ½µÄĶ¼ŠĪ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĖ³ĄūĶعż”°¹ś¼ŅĪÄĆ÷³ĒŹŠ”±ŃéŹÕ£¬¶«ÓŖŹŠÕžø®Äā¶Ō³ĒĒų²æ·ÖĀ·¶ĪµÄČĖŠŠµĄµŲש”¢ĀĢ»Æ“ų”¢ÅÅĖ®¹ÜµĄµČ¹«ÓĆÉ菩ȫĆęøüŠĀøÄŌģ£¬øł¾ŻŹŠÕž½ØÉčµÄŠčŅŖ£¬ŠčŌŚ40ĢģÄŚĶź³É¹¤³Ģ£®ĻÖÓŠ¼×”¢ŅŅĮ½øö¹¤³Ģ¶ÓÓŠŅā³Š°üÕāĻī¹¤³Ģ£¬¾µ÷²éÖŖµĄ£¬ŅŅ¹¤³Ģ¶Óµ„¶ĄĶź³É“ĖĻī¹¤³ĢµÄŹ±¼äŹĒ¼×¹¤³Ģ¶Óµ„¶ĄĶź³É“ĖĻī¹¤³ĢŹ±¼äµÄ2±¶£¬Čō¼×”¢ŅŅĮ½¹¤³Ģ¶ÓŗĻ×÷Ö»Šč10ĢģĶź³É£®
£Ø1£©¼×”¢ŅŅĮ½øö¹¤³Ģ¶Óµ„¶ĄĶź³É“ĖĻī¹¤³Ģø÷Šč¶ąÉŁĢģ£æ
£Ø2£©Čō¼×¹¤³Ģ¶ÓĆæĢģµÄ¹¤³Ģ·ŃÓĆŹĒ4.5ĶņŌŖ£¬ŅŅ¹¤³Ģ¶ÓĆæĢģµÄ¹¤³Ģ·ŃÓĆŹĒ2.5ĶņŌŖ£¬ĒėÄćÉč¼ĘŅ»ÖÖ·½°ø£¬¼ČÄÜ°“Ź±Ķź¹¤£¬ÓÖÄÜŹ¹¹¤³Ģ·ŃÓĆ×īÉŁ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬ŅŌABĪŖÖ±¾¶µÄ”ŃO½»BCÓŚµćD£¬¹żµćD×÷DE”ĶACÓŚE½»ABµÄŃÓ³¤ĻßÓŚµćF£®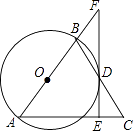
£Ø1£©ĒóÖ¤£ŗEFŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©ČōAE=6£¬FB=4£¬Ēó”ŃOµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£®ABŹĒ”ŃOµÄÖ±¾¶£¬EĪŖĻŅAPÉĻŅ»µć£¬¹żµćE×÷EC”ĶABÓŚµćC£¬ŃÓ³¤CEÖĮµćF£¬Į¬½ÓFP£¬Ź¹”ĻFPE=”ĻFEP£¬CF½»”ŃOÓŚµćD£® 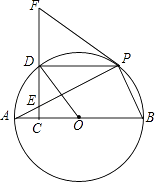
£Ø1£©Ö¤Ć÷£ŗFPŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©ČōĖıߊĪOBPDŹĒĮāŠĪ£¬Ö¤Ć÷£ŗFD=ED£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬OĪŖ”÷ABCÄŚŅ»µć£¬OD”ĶABÓŚµćD£¬OE”ĶACÓŚµćE£¬OF”ĶBCÓŚµćF£¬ČōOD£½OE£½OF£¬Į¬½ÓOA£¬OB£¬OC£¬ĻĀĮŠ½įĀŪ²»Ņ»¶ØÕżČ·µÄŹĒ( )
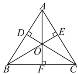
A. ”÷BOD”Õ”÷BOF B. ”ĻOAD£½”ĻOBF
C. ”ĻCOE£½”ĻCOF D. AD£½AE
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com