
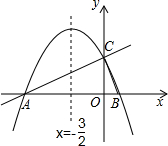 如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B.
如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B.分析 (1)①先求的直线y=$\frac{1}{2}$x+2与x轴交点的坐标,然后利用抛物线的对称性可求得点B的坐标;②设抛物线的解析式为y=y=a(x+4)(x-1),然后将点C的坐标代入即可求得a的值;
(2)设点P、Q的横坐标为m,分别求得点P、Q的纵坐标,从而可得到线段PQ=$-\frac{1}{2}$m2-2m,然后利用三角形的面积公式可求得S△PAC=$\frac{1}{2}$×PQ×4,然后利用配方法可求得△PAC的面积的最大值以及此时m的值,从而可求得点P的坐标;
(3)首先可证明△ABC∽△ACO∽△CBO,然后分以下几种情况分类讨论即可:①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;②根据抛物线的对称性,当M(-3,2)时,△MAN∽△ABC; ④当点M在第四象限时,解题时,需要注意相似三角形的对应关系.
解答 解:(1)①y=$\frac{1}{2}x+2$当x=0时,y=2,当y=0时,x=-4,
∴C(0,2),A(-4,0),
由抛物线的对称性可知:点A与点B关于x=-$\frac{3}{2}$对称,
∴点B的坐标为1,0).
②∵抛物线y=ax2+bx+c过A(-4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x-1),
又∵抛物线过点C(0,2),
∴2=-4a
∴a=$-\frac{1}{2}$
∴y=$-\frac{1}{2}$x2$-\frac{3}{2}$x+2.
(2)设P(m,$-\frac{1}{2}$m2$-\frac{3}{2}$m+2).
过点P作PQ⊥x轴交AC于点Q,
∴Q(m,$\frac{1}{2}$m+2),
∴PQ=$-\frac{1}{2}$m2$-\frac{3}{2}$m+2-($\frac{1}{2}$m+2)
=$-\frac{1}{2}$m2-2m,
∵S△PAC=$\frac{1}{2}$×PQ×4,
=2PQ=-m2-4m=-(m+2)2+4,
∴当m=-2时,△PAC的面积有最大值是4,
此时P(-2,3).
(3)方法一:
在Rt△AOC中,tan∠CAO=$\frac{1}{2}$在Rt△BOC中,tan∠BCO=$\frac{1}{2}$,
∴∠CAO=∠BCO,
∵∠BCO+∠OBC=90°,
∴∠CAO+∠OBC=90°,
∴∠ACB=90°,
∴△ABC∽△ACO∽△CBO,
如下图:
①当M点与C点重合,即M(0,2)时,△MAN∽△BAC;
②根据抛物线的对称性,当M(-3,2)时,△MAN∽△ABC;
③当点M在第四象限时,设M(n,$-\frac{1}{2}$n2$-\frac{3}{2}$n+2),则N(n,0)
∴MN=$\frac{1}{2}$n2+$\frac{3}{2}$n-2,AN=n+4
当$\frac{MN}{AN}=\frac{1}{2}$时,MN=$\frac{1}{2}$AN,即$\frac{1}{2}$n2+$\frac{3}{2}$n-2=$\frac{1}{2}$(n+4)
整理得:n2+2n-8=0
解得:n1=-4(舍),n2=2
∴M(2,-3);
当$\frac{MN}{AN}=\frac{2}{1}$时,MN=2AN,即$\frac{1}{2}$n2+$\frac{3}{2}$n-2=2(n+4),
整理得:n2-n-20=0
解得:n1=-4(舍),n2=5,
∴M(5,-18).
综上所述:存在M1(0,2),M2(-3,2),M3(2,-3),M4(5,-18),使得以点A、M、N为顶点的三角形与△ABC相似.
方法二:
∵A(-4,0),B(1,0),C(0,2),
∴KAC×KBC=-1,
∴AC⊥BC,MN⊥x轴,
若以点A、M、N为顶点的三角形与△ABC相似,
则$\frac{MN}{NA}=\frac{AC}{BC}$,$\frac{MN}{NA}=\frac{BC}{AC}$,
设M(2t,-2t2-3t+2),
∴N(2t,0),
①|$\frac{2{t}^{2}+3t-2}{2t+4}$|=$\frac{\sqrt{5}}{2\sqrt{5}}$,
∴|$\frac{2t-1}{2}$|=$\frac{1}{2}$,
∴2t1=0,2t2=2,
②|$\frac{2{t}^{2}+3t-2}{2t+4}$|=$\frac{2\sqrt{5}}{\sqrt{5}}$,
∴|$\frac{2t-1}{2}$|=2,∴2t1=5,2t2=-3,
综上所述:存在M1(0,2),M2(-3,2),M3(2,-3),M4(5,-18),使得以点A、M、N为顶点的三角形与△ABC相似.
点评 本题主要考查的是二次函数与相似三角形的综合应用,难度较大,解答本题需要同学们熟练掌握二次函数和相似三角形的相关性质.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题

| A. | 2004年至2013年雾霾天数最少的是2010年 | |
| B. | 2012年到2013年雾霾天数上升明显 | |
| C. | 2004年至2012年雾霾天数呈下降趋势 | |
| D. | 2013年1-10月雾霾天数已超200天,可见环境污染越来越严重 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 第1行 | 1 2 3 |
| 第2行 | 4 5 6 7 8 |
| 第3行 | 9 10 11 12 13 14 15 |
| 第4行 | 16 17 18 19 20 21 22 23 24 |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形网格中:
如图,在边长为1个单位长度的小正方形网格中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
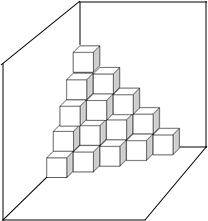 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com