
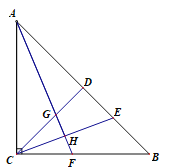
【题目】等腰Rt△ABC,点D为斜边AB上的中点,点E在线段BD上,连结CD,CE,作AH⊥CE,垂足为H,交CD于点G,AH的延长线交BC于点F.
(1)求证:△ADG≌△CDE.
(2)若点H恰好为CE的中点,求证:∠CGF=∠CFG.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据已知条件可得出AD=CD=BD,∠CGH+∠GCH=∠AGD+∠GAD=90°,继而得出∠GAD=∠GCH,从而结论得以证明.
(2)由已知条件可得,∠CAH=∠EAH,继而得出∠AGD=∠=CGH=∠CFG.
解:(1)在等腰Rt△ABC中,
∵ 点D为斜边AB上的中点
∴ CD=![]() AB,CD⊥AB
AB,CD⊥AB
∵AD=![]() AB
AB
∴AD=CD
∵ CD⊥AB
∴ ∠ADG=∠CDE=90°
∵AH⊥CE
∴∠CGH+∠GCH=90°
∵∠AGD+∠GAD=90°
又∵∠AGD=∠CGH
∴∠GAD=∠GCH
在△△ADG和△CDE中
∵∠ADG=∠CDE=90°,AD=CD,∠GAD=∠GCH
∴△ADG≌△CDE…
(2)∵AH⊥CE,点H为CE的中点
∴AC=AE
∴∠CAH=∠EAH
∵∠CAH+∠AFC=90°
∠EAH+∠AGD=90°
∴∠AFC=∠AGD
∵∠AGD=∠CGH
∴∠AFC=∠CGH
即∠CGF=∠CFG.


科目:初中数学 来源: 题型:
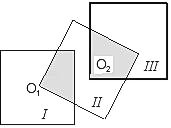
【题目】如图,有若干个边长为2的正方形,若正方形的一个顶点是正方形Ⅰ的中心O1,如图所示,类似的正方形Ⅲ的一个顶点是正方形Ⅱ的中心O2,并且正方形Ⅰ与正方形Ⅲ不重叠,如果若干个正方形都按这种方法拼接,需要m个正方形能使拼接处的图形的阴影部分的面积等于一个正方形的面积.现有一拋物线y=mx2+nx+3,其顶点在x轴上,则该抛物线的对称轴为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
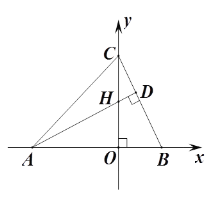
【题目】如图,在平面直角坐标系中AD⊥BC,垂足为D,交y轴于点H,直线BC的解析式为y=-2x+4.点H(0,2),
(1)求证:△AOH≌△COB;
(2)求D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠B=30°,CD,CE分别是AB边上的中线和高.

(1)求证:AE=ED;
(2)若AC=2,求△CDE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为营造浓厚的创建全国文明城市氛围,东营市某中学委托制衣厂制作“最美东营人”和“最美志愿者”两款文化衫.若制作“最美东营人”文化衫2件,“最美志愿者”文化衫3件,共需90元;制作“最美东营人”文化衫3件,“最美志愿者”5件,共需145元.
(1)求“最美东营人”和“最美志愿者”两款文化衫每件各多少元?
(2)若该中学要购进“最美东营人”和“最美志愿者”两款文化衫共90件,总费用少于1595元,并且“最美东营人”文化衫的数量少于“最美志愿者”文化衫的数量,那么该中学有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',下列结论:①△BO'A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为6;③∠AOB=150°;④S△BOC=12+6![]() ; ⑤S四边形AOBO′=24+12
; ⑤S四边形AOBO′=24+12![]() .其中正确的结论是_____.(填序号)
.其中正确的结论是_____.(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com