
【题目】解下列方程:
(1)![]() =3.
=3.
(2)(y+2)2=(3y﹣1)2.
(3)(x﹣2)(x+5)=8.
(4)(2x+1)2=﹣6x﹣3.
(5)2x2﹣3x﹣2=0.
(6)4x2﹣12x﹣1=0(配方法).
【答案】(1) x1=0,x2=﹣6;(2) y1=﹣![]() ,y2=
,y2=![]() ;(3) x1=3,x2=﹣6;(4) x1=﹣
;(3) x1=3,x2=﹣6;(4) x1=﹣![]() ,x2=﹣2;(5)x1=﹣
,x2=﹣2;(5)x1=﹣![]() ,x2=2;(6) x1=
,x2=2;(6) x1=![]() ,x2=
,x2=![]() .
.
【解析】
(1)变形后开方,即可得出两个一元一次方程,求出方程的解即可;
(2)移项后分解因式,开方,即可得出两个一元一次方程,求出方程的解即可;
(3)整理后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(4)移向后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(5)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(6)移项,系数化成1,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
(1)![]() =3,
=3,
(x+3)2=9,
x+3=±3,
x1=0,x2=﹣6;
(2)(y+2)2=(3y﹣1)2.
(y+2)2﹣(3y﹣1)2,=0,
[(y+2)+(3y﹣1)][(y+2)﹣(3y﹣1)]=0,
(y+2)+(3y﹣1)=0,(y+2)﹣(3y﹣1)=0,
y1=﹣![]() ,y2=
,y2=![]() ;
;
(3)(x﹣2)(x+5)=8.
整理得:x2+3x﹣18=0,
(x﹣3)(x+6)=0,
x﹣3=0,x+6=0,
x1=3,x2=﹣6;
(4)(2x+1)2=﹣6x﹣3,
(2x+1)2+3(2x+1)=0,
(2x+1)(2x+1+3)=0,
2x+1=0,2x+1+3=0,
x1=﹣![]() ,x2=﹣2;
,x2=﹣2;
(5)2x2﹣3x﹣2=0,
(2x+1)(x﹣2)=0,
2x+1=0,x﹣2=0,
x1=﹣![]() ,x2=2;
,x2=2;
(6)4x2﹣12x﹣1=0
4x2﹣12x=1,
x2﹣3x+(![]() )2=
)2=![]() +(
+(![]() )2,
)2,
(x﹣![]() )2=
)2=![]() ,
,
x﹣![]() =±
=±![]() ,
,
x1=![]() ,x2=
,x2=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一架云梯AB的长25 m,斜靠在一面墙上,梯子靠墙的一端A距地面距离AC为24 m.
(1)这个梯子底端B离墙的距离BC有多少米?
(2)如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向也滑动了4 m吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm. 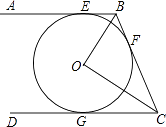
(1)求证:BO⊥CO;
(2)求BE和CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
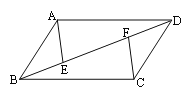
【题目】如图,四边形ABCD中,AB=CD,AB∥CD,点E、F在线段BD上,且BE=DF,连接AE、CF.
(1)指出线段AE与CF的关系,并说明理由;
(2)若将题中的条件“点E、F在线段BD上”改为“点E、F在直线BD上” ,那么(1)中的结论还一定能成立吗?若能,直接写出结论;若不能,请举出反例加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
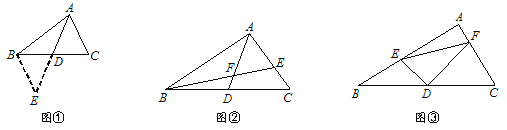
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
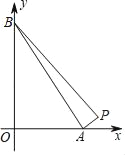
【题目】由点P(14,1),A(a,0),B(0,a)确定的△PAB的面积为18.
(1)如图,若0<a<14,求a的值.
(2)如果a>14,请画图并求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABE=∠ACD=Rt∠,AE=AD,∠ABC=∠ACB.求证:∠BAE=∠CAD.
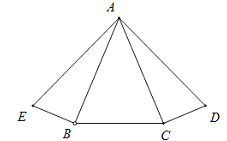
请补全证明过程,并在括号里写上理由.
证明:在△ABC中,
∵∠ABC=∠ACB
∴AB= ( )
在Rt△ABE和Rt△ACD中,
∵ =AC, =AD
∴Rt△ABE≌Rt△ACD( )
∴∠BAE=∠CAD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2 ![]() ,∠C=120°,以点C为圆心的
,∠C=120°,以点C为圆心的 ![]() 与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 .
与AB,AD分别相切于点G,H,与BC,CD分别相交于点E,F.若用扇形CEF作一个圆锥的侧面,则这个圆锥的高是 . 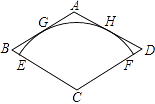
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com