
【题目】如图所示,已知CE⊥AB于点E,BD⊥AC于点D,BD与CE交于点O,且AO平分∠BAC.
(1)图中有多少对全等三角形?请你一一列举出来(不要求说明理由).
(2)小明说:欲说明BE=CD,可先说明△AOE≌△AOD得到AE=AD,再说明△ADB≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?请仿照小明的说法具体说一说你的想法.

【答案】(1)见解析;(2)正确,理由见解析.
【解析】
(1)根据全等三角形的判定得出即可.
(2)求出∠EAO=∠DAO,∠AEO=∠ADO=90°,根据AAS证△AEO≌△ADO,推出AE=AD,根据ASA证△ADB≌△AEC,推出AB=AC即可.
(3)根据垂直和角平分线性质得出OE=OD,∠BEO=∠CDO=90°,根据ASA推出△BEO≌△CDO即可.
(1)共4对,分别是△AOE≌△AOD,△BOE≌△COD,△AOB≌△AOC,△ABD≌△ACE.
(2)正确.
因为CE⊥AB于点E,BD⊥AC于点D,
所以∠AEO=∠ADO.
因为AO平分∠BAC,
所以∠OAE=∠OAD.
在△AOE和△AOD中,
因为∠AEO=∠ADO,∠OAE=∠OAD,AO=AO,
所以△AOE≌△AOD,
所以AE=AD.
在△ADB和△AEC中,
因为∠BAD=∠CAE,AD=AE,∠ADB=∠AEC,
所以△ADB≌△AEC,
所以AB=AC,
所以AB-AE=AC-AD,
即BE=CD.
(3)答案不唯一,如可先说明△AOE≌△AOD,得到OE=OD,再说明△BOE≌△COD,得到BE=CD.


科目:初中数学 来源: 题型:
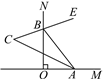
【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠ABN,BE的反向延长线与∠BAO的平分线交于点C.
(1)当点A,B移动后,∠BAO=45°时,∠C=________;
(2)当点A,B移动后,∠BAO=60°时,∠C=________;
(3)由(1)(2)猜想∠C是否随点A,B的移动而发生变化,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
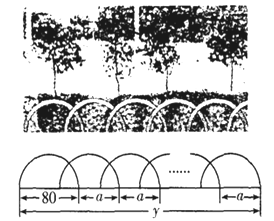
【题目】如图,某花园护栏是用直径为![]() 厘米的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度就增加
厘米的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度就增加![]() 厘米
厘米![]() .设半圆形条钢的总个数为
.设半圆形条钢的总个数为![]() (
(![]() 为正整数),护栏总长度为
为正整数),护栏总长度为![]() 厘米.
厘米.
(1)当![]() ,
,![]() 时,护栏总长度
时,护栏总长度![]() 为________厘米;
为________厘米;
(2)当![]() 时,用含
时,用含![]() 的代数式表示护栏总长度
的代数式表示护栏总长度![]() (结果要化简);
(结果要化简);
(3)在第(2)题的条件下,若要使护栏总长度保持不变,而把![]() 改为50
改为50![]() ,就要共用
,就要共用![]() 个半圆形条钢,请求出
个半圆形条钢,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是( )

A. BC=EC,∠B=∠E B. BC=EC,AC=DC
C. ∠B=∠E,∠A=∠D D. BC=EC,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 三对数值中,________是方程x+y=3的解,________是方程3x+2y=5的解,________是方程组
三对数值中,________是方程x+y=3的解,________是方程3x+2y=5的解,________是方程组![]() 的解.(填序号)
的解.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
![]()
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(c2012防城港)某奶品生产企业,2010年对铁锌牛奶、酸牛奶、纯牛奶三个品种的生产情况进行了统计,绘制了图1、2的统计图,请根据图中信息解答下列问题: 
(1)酸牛奶生产了多少万吨?把图1补充完整;酸牛奶在图2所对应的圆心角是多少度?
(2)由于市场不断需求,据统计,2011年的生产量比2010年增长20%,按照这样的增长速度,请你估算2012年酸牛奶的生产量是多少万吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A的坐标为(﹣2,﹣1),点B的坐标为(0,﹣2),若将线段AB平移至A′B′的位置,点A′的坐标为(a,2),点B′的坐标为(1,b),则a+b的值为( )
A. 0 B. 2 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com