练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
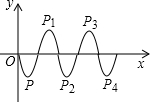
    4．如图，将顶点为P（1，-2），且过原点的抛物线y的一部分沿x轴翻折并向右平移2个单位长度，得到抛物线y1，其顶点为P1，然后将抛物线y1沿x轴翻折并向右平移2个单位长度，得到抛物线y2，其顶点为P2；…，如此进行下去，直至得到抛物线y2016，则点P2016坐标为（4033，-2）．

    分析 根据图形的变换，可得规律：第n次平移变换点的横坐标是2n+1，偶数次变换平移点的纵坐标是-2，奇数次变换平移点的坐标是2，可得答案．

    解答 解：第一次变换平移点的坐标是（3，2），
    第二次变换平移点的坐标是（5，-2），
    第三次变换平移点的坐标是（7，2，）
    第n次平移变换点的横坐标是2n+1，偶数次变换平移点的纵坐标是-2，奇数次变换平移点的坐标是2，
    点P2016坐标为（4033，-2），
    故答案为：（4033，-2）．

    点评 本题考查了二次函数图象与几何变换，观察发现规律是解题关键，规律：第n次平移变换点的横坐标是2n+1，偶数次变换平移点的纵坐标是-2，奇数次变换平移点的坐标是2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．如图，在矩形ABCD中，AC是对角线，sin∠ACB=$\frac{\sqrt{5}}{5}$，BE⊥AC，将△ABE绕A逆时针旋转使AE落在AD上，E的对应点为M，B的对应点为N．设△AMN向右平移的距离是x，△AMN与△ACD重合的面积为y，y关于x的函数图象如图所示．（其中0＜x≤a，a＜x≤b，b＜x≤c，函数图象不同）

    （1）△AMN的面积是4；
    （2）求y与x的函数关系式；
    （3）y的值能否为3，若能，求出x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．某商品的进价为每件40元，当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件，在确保盈利的前提下，解答下列问题：
    （1）求降价前每星期的销售利润；
    （2）若设每件降价x元，每星期售出商品的利润为y元，请写出y与x的函数关系式，并直接写出自变量x的取值范围；
    （3）当降价多少元时，每星期的利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．在平面直角坐标系xOy中，把抛物线C1：y=x2-4沿x轴向右平移m（m＞0）个单位长度，得抛物线C2，C1和C2的交点为点M（如图1）
    （1）用含m的式子来表示抛物线C2的解析式和点M的坐标；
    （2）定义：像C1和C2两条抛物线，是把其中一条沿水平方向向左（像向右）平移得到另一条．若两抛物线的顶点P、Q以及交点M满足∠PMQ=90°，则这样的两条抛物线互为“和谐线”．
    ①求抛物线C1：y=x2-4的和谐线；
    ②如图2，抛物线C1：y=x2-4与x轴正半轴的交点为A，与它的和谐线的交点为M（点M在第四象限），连接MA，过点M作MH⊥x轴，在x轴上存在一点N，使∠ONM+∠AMH=45°，求点N的坐标

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

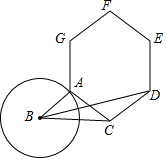    19．如图，BC=2，A为半径为1的⊙B上一点，连接AC，在AC上方作一个正六边形ACDEFG，连接BD，则BD的最大值为$2\sqrt{3}+1$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，矩形OABC中，OA=3，OC=5，OA，OC分别在x轴，y轴上，D是边CB上的一个动点（不与C，B重合），反比例函数y=$\frac{k}{x}$（k＞0）的图象经过点D且与边BA交于点E，连接DE．
    （1）若△BDE的面积为$\frac{10}{3}$，求k的值；
    （2）设直线DE的解析式为y=mx+n，求证：m为定值；
    （3）是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．将两张完全相同的平行四边形纸片按如图1所示放置（其中点E在BC上，点A在BG上，AB=BE=4，BC=BG=$2\sqrt{3}+2$，∠B=60°），?ABCD固定不动，将?GBEF绕点B顺时针旋转，旋转角为a（0°＜a＜360°）．
    （1）如图1，连接AF，求AF的长．
    （2）如图2，当?GBEF绕点B旋转到点F与点D重合时，AD与BG相交于点M，BC与ED相交于点N，求证：四边形BMDN是菱形．
    （3）如图3，在旋转过程中，当旋转角a为多少度时，以点C，G，D，F为顶点的四边形是正方形？是矩形？请给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．问题情境：如图①，P是⊙O外的一点，直线PO分别交⊙O于点A、B，可以发现PA是点P到⊙O上的点的最短距离．
    （1）直接运用：如图②，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是弧CD上的一个动点，连接AP，则AP的最小值是$\sqrt{5}$-1．
    （2）构造运用：如图③，在边长为8的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，请求出A′C长度的最小值．
    （3）综合运用：如图④，平面直角坐标系中，分别以点A（-2，3），B（3，4）为圆心，分别以1、2为半径作⊙A、⊙B，M、N分别是⊙A、⊙B上的动点，P为x轴上的动点，则PM+PN的最小值等于$\sqrt{74}$-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．甲、乙两车从相距100km的A、B两站同向开出，匀速前进，当甲车追上乙车时，甲、乙两车①所用时间同，②所行驶路相同，③甲比乙多行100km，④甲、乙两车共行驶了100km．其中正确的是（　　）
    A．①③B．①②④C．①④D．②③

    查看答案和解析>>

    同步练习册答案