
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
 n��ȡ�ߺ�ʣ
n��ȡ�ߺ�ʣ| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 2n-1 |
| 3n |
| 2n |
| 3n |
| 2n |
| 3n |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2n |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3n |

| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 2n-1 |
| 3n |
| 2n |
| 3n |
| 2n |
| 3n |


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 2n |
| 2 |
| 3 |

| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
| 3n |

| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
| 81 |
| 2n-1 |
| 3n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�γ������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����ͼ������ʾ������������ϵ��Ҳ��������������������ϵ������ͼ��������ͼ��֮��Ĺ�ϵ������˼�뷽����Ϊ���ν�ϣ����Ǹ�ѧ���ĵ�9�¡���ʽ�˷�����ʽ�ֽ⡷�ͺܺõ���������һ˼�뷽���������������ν�ϵ�˼��������������
��1����ͼ��һ���߳�Ϊ1�������Σ�����ȡ�����������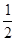 ��
�� ��
��
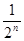 ������ͼʾ���ǿ���֪����
������ͼʾ���ǿ���֪����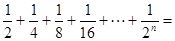 ��
��

����������ʽ���㣺 ��
��
��2�����㣺 ��
��
��3�����㣺 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013�������ѧ��Ԫ���Ų��Ծ�-ƽ���ʽ�������棩 ���ͣ������
����ͼ������ʾ������������ϵ��Ҳ��������������������ϵ������ͼ��������ͼ��֮��Ĺ�ϵ������˼�뷽����Ϊ���ν�ϣ����Ǹ�ѧ���ġ���������˷���ʽ���ͺܺõ���������һ˼�뷽���������������ν�ϵ�˼��������������
��ͼ��һ���߳�Ϊ1�������Σ�����ȡ�����ε�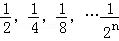 ������ͼʾ���ǿ���֪������һ��ȡ��
������ͼʾ���ǿ���֪������һ��ȡ�� ��ʣ
��ʣ ����
���� =1��
=1�� ��ǰ����ȡ��
��ǰ����ȡ�� +
+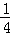 ��ʣ
��ʣ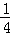 ����
���� +
+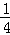 =1��
=1��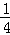 ��ǰ����ȡ��
��ǰ����ȡ��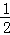 +
+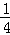 +
+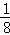 ��ʣ
��ʣ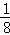 ����
����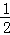 +
+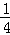 +
+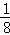 =1��
=1��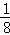 ����ǰn��ȡ�ߺ�ʣ��_________��������_________��=��_________����
����ǰn��ȡ�ߺ�ʣ��_________��������_________��=��_________����
�����������㣺
��1��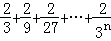 =��_________����
=��_________����
��2��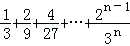 =��_________����
=��_________����
��3��2��22��23��24��25��26������22011+22012������д��������̣�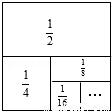
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�콭��ʡ��̶ʵ��ѧУ���꼶��ѧ�����п�����ѧ���������棩 ���ͣ������
����ͼ������ʾ������������ϵ��Ҳ��������������������ϵ������ͼ��������ͼ��֮��Ĺ�ϵ������˼�뷽����Ϊ���ν�ϣ����Ǹ�ѧ���ġ���������˷���ʽ���ͺܺõ���������һ˼�뷽���������������ν�ϵ�˼��������������
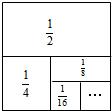
��ͼ��һ���߳�Ϊ1�������Σ�����ȡ�����ε�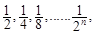 ����ͼʾ���ǿ���֪������һ��ȡ��
����ͼʾ���ǿ���֪������һ��ȡ��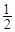 ��ʣ
��ʣ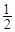 ����
����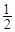 =1��
=1��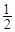 ��ǰ����ȡ��
��ǰ����ȡ��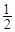 +
+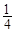 ��ʣ
��ʣ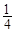 ����
����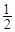 +
+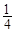 =1��
=1��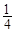 ��ǰ����ȡ��
��ǰ����ȡ��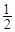 +
+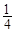 +
+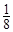 ��ʣ
��ʣ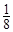 ����
����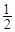 +
+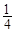 +
+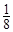 =1��
=1��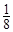 ������ǰn��ȡ�ߺ�ʣ
��
������ǰn��ȡ�ߺ�ʣ
��
�� = ��
�����������㣺
(1) 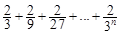 =
��
=
��
(2) 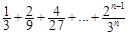 =
��
=
��
(3) 2��22��23��24��25��26������22011+22012 ������д��������̣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com