
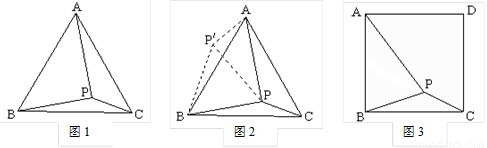
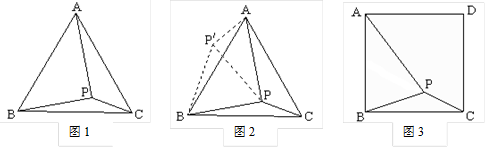
1.请阅读材料并填空:
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1.求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2).连结PP′.
根据李明同学的思路,进一步思考后可求得∠BPC=____°,等边△ABC的边长为____.
2.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=,BP=,PC=1.求∠BPC的度数和正方形ABCD的边长.
1.150°,
2.如图,将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A. ……3分
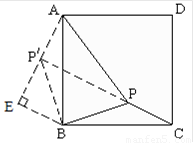
∴AP′=PC=1,BP=BP′=.
连结PP′,在Rt△BP′P中,∵ BP=BP′=,∠PBP′=90°,
∴ PP′=2,∠BP′P=45°. …………4分
在△AP′P中, AP′=PC=1,PP′=2,AP=,∵ 12+22=()2,即AP′ 2+PP′ 2=AP2.
∴ △AP′P是直角三角形,即∠AP′P=90°. …………5分
∴∠AP′B=∠AP′P+∠BP′P=135°.
∴ ∠BPC=∠AP′B=135°. …………6分
过点B作BE⊥AP′交AP′的延长线于点E.
则∠EP′B=45°,∴ EP′=BE=BP′=1,∴AE=2.
∴在Rt△ABE中,由勾股定理,得AB=. …………8分
∴∠BPC=135°,正方形边长为.
【解析】略


科目:初中数学 来源: 题型:阅读理解
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
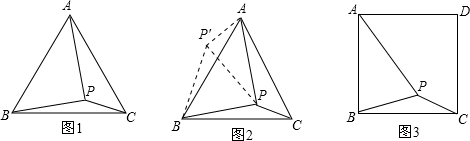
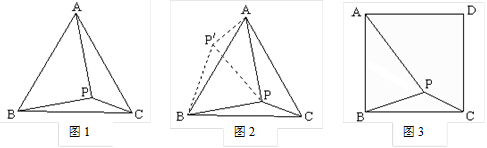
1.请阅读材料并填空:
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1.求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2).连结PP′.
根据李明同学的思路,进一步思考后可求得∠BPC=____°,等边△ABC的边长为____.
2.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=,BP=,PC=1.求∠BPC的度数和正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,PC=1.求∠BPC的度数和等边三角形ABC的边长.
,PC=1.求∠BPC的度数和等边三角形ABC的边长. ,BP=
,BP= ,PC=1.求∠BPC的度数和正方形ABCD的边长.
,PC=1.求∠BPC的度数和正方形ABCD的边长.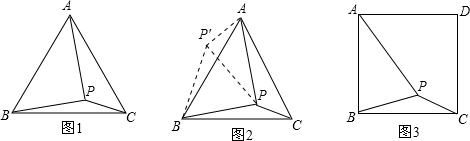
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com