在平面直角坐标系中，已知y=﹣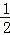
x2+bx+c（b、c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），点C的坐标为（4，3），直角顶点B在第四象限．
（1）如图，若抛物线经过A、B两点，求抛物线的解析式．
（2）平移（1）中的抛物线，使顶点P在直线AC上并沿AC方向滑动距离为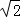
时，试证明：平移后的抛物线与直线AC交于x轴上的同一点．
（3）在（2）的情况下，若沿AC方向任意滑动时，设抛物线与直线AC的另一交点为Q，取BC的中点N，试探究NP+BQ是否存在最小值？若存在，求出该最小值；若不存在，请说明理由．
名校课堂系列答案科目：初中数学 来源： 题型：
某公司生产的某种产
品每件成本为40元，经市场调查整理出如下信息：
①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：
| 时间（第x天） | 1 | 3 | 6 | 10 | … |
| 日销售量（m件） | 198 | 194 |
| 180 | … |
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：
| 时间（第x天） | 1≤x＜50 | 50≤x≤90 |
| 销售价格（元/件） | x+60 | 100 |
（1）求m关于x的一次函数表达式；
（2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格-每件成本）】
（3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB=2米，BP=3米，PD=12米，那么该古城墙的高度CD是 米．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系内，O为原点，点A的坐标为（﹣3，0），经过A、O两点作半径为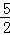
的⊙C，交y轴的负半轴于点B．
（1）求B点的坐标；
（2）过B点作⊙C的切线交x轴于点D，求直线BD的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
在一个不透明的袋子中，装有红球、黄球、蓝球、白球各1个,这些球除颜
色外无其他差别,从袋中随机取出一个球,取出红球的概率为（ C ）
A.
B. C.
D.1
查看答案和解析>>
科目：初中数学 来源： 题型：
如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND
为直径作半圆,则阴影部分面积为( )
|
|
| 第12题 |
A.9
B.18 C.36 D.72
查看答案和解析>>
科目：初中数学 来源：2014-2015学年江苏江阴第一中学九年级3月月考数学试卷（解析版） 题型：解答题
（本题满分9分）
操作：小英准备制作一个表面积为6cm2的正方体纸盒，现选用一些废弃的纸片进行如下设计：
说明：
方案一：图形中的圆过点A.B.C；
方案二：直角三角形的两直角边与展开图左下角的正方形边重合，斜边经过两个正方形的顶点．
纸片利用率=
×100%
发现：（1）小英发现方案一中的点A.B恰好为该圆一直径的两个端点．你认为小英的这个发现是否正确，请说明理由．
（2）小英通过计算，发现方案一中纸片的利用率仅约为38.2%．请帮忙计算方案二的利用率，并写出求解过程．（结果精确到0.1%）
探究：（3）小英感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．（结果精确到0.1%）
说明：方案三中的每条边均过其中两个正方形的顶点．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年江苏海安县城东镇韩洋初中九年级上学期学业分析数学试卷（解析版） 题型：填空题
一辆汽车，新车购买价20万元，第一年使用后折旧20%，以后该车的年折旧率有所变化，但它在第二、三年的年折旧率都为x.已知在第三年年末，这辆车折旧后价值11.56 万元，可列方程为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
+
=
÷
=3