
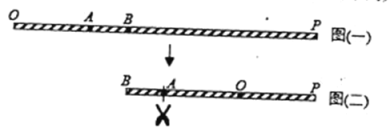
【题目】如图(一),![]() 为一条拉直的细线,
为一条拉直的细线,![]() 两点在
两点在![]() 上,且
上,且![]() . 若先固定
. 若先固定![]() 点,将
点,将![]() 折向
折向![]() ,使得
,使得![]() 重迭在BP上,如图(二);再从图(二)的
重迭在BP上,如图(二);再从图(二)的![]() 点及与
点及与![]() 点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为( )
点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】![]() 城有肥料
城有肥料![]() 吨,
吨,![]() 城有肥料
城有肥料![]() 吨,现要把这些肥料全部运往
吨,现要把这些肥料全部运往![]() 、
、![]() 两乡.从
两乡.从![]() 城运往
城运往![]() 、
、![]() 两乡运肥料的费用分别是每吨
两乡运肥料的费用分别是每吨![]() 元和
元和![]() 元,从
元,从![]() 城往
城往![]() 、
、![]() 两乡运肥料的费用分别为每吨
两乡运肥料的费用分别为每吨![]() 元和
元和![]() 元,现在
元,现在![]() 乡需要肥料
乡需要肥料![]() 吨,
吨,![]() 乡需要肥料
乡需要肥料![]() 吨,设
吨,设![]() 城运往
城运往![]() 乡的肥料量为
乡的肥料量为![]() 吨,总运费为
吨,总运费为![]() 元.
元.
(1)写出总运费![]() 元与
元与![]() 之间的关系式;
之间的关系式;
(2)当总费用为![]() 元,求从
元,求从![]() 、
、![]() 城分别调运
城分别调运![]() 、
、![]() 两乡各多少吨?
两乡各多少吨?
(3)怎样调运化肥,可使总运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
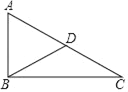
【题目】如图,在△ABC中,∠ABC=90°,BD为AC边上的中线.
(1)按如下要求尺规作图,保留作图痕迹,标注相应的字母:过点C作直线CE,使CE⊥BC于点C,交BD的延长线于点E,连接AE;
(2)求证:四边形ABCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生课余生活,计划开设以下课外活动项目:A—版画,B—机器人,C—航模,D—园艺种植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生必须选且只能选一个项目),并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
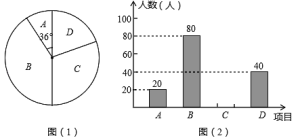
(1)这次被调查的学生共有 人;扇形统计图中,选“D—园艺种植”的学生人数所占圆心角的度数是 °
(2)请你将条形统计图补充完整;
(3)若该校学生总数为1000人,试估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
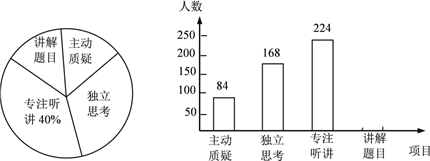
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)~(2)题:
数学课上,老师出示了一道题:如图1,将一个直角三角板![]() 的直角边
的直角边![]() 摆放在直线
摆放在直线![]() 上,然后以直角顶点
上,然后以直角顶点![]() 为旋转中心顺时针旋转这个三角板.若射线
为旋转中心顺时针旋转这个三角板.若射线![]() 平分
平分![]() 、探究
、探究![]() 和
和![]() 的数量关系,并说明经过一段时间的思考后,同学们开始了交流:
的数量关系,并说明经过一段时间的思考后,同学们开始了交流:
小明:我根据老师的叙述画出图2,并计算出当![]() 时,
时,![]() 的度数是
的度数是![]() ;
;
小红:在小明的图形中,点![]() 、
、![]() 都在
都在![]() 的上方,我发现,在这种情况下,
的上方,我发现,在这种情况下,![]() 始终在
始终在![]() 的内部.若设
的内部.若设![]() 的度数是
的度数是![]() ,通过计算,
,通过计算,![]() 的度数可以用含
的度数可以用含![]() 的式子表示,得到
的式子表示,得到![]() 和
和![]() 的数量关系是
的数量关系是![]() ;
;
小华:我除了画小明的这种图形,还画了其余几种,也分别得出![]() 和
和![]() 的数量关系,从而解决了老师提出的问题.
的数量关系,从而解决了老师提出的问题.
老师:这些同学都先画出图形,再解决问题,这体现了图形的直性,但要注意一点,在初中阶段我们研究的角都是小于![]() 的.随着大家交流的深入,点
的.随着大家交流的深入,点![]() 的位置由
的位置由![]() 上方到直线
上方到直线![]() 外,
外,![]() 的值由数字到字母,这体现了从特殊到一般的思想,同学们再根据小华所说的进行探究,还能归纳出其他的数学思想方法!
的值由数字到字母,这体现了从特殊到一般的思想,同学们再根据小华所说的进行探究,还能归纳出其他的数学思想方法!
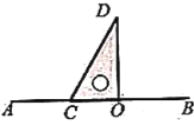
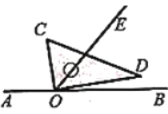
图1 图2
(1)如图2,点![]() 、
、![]() 都在
都在![]() 上方,
上方,![]() .
.
①用含![]() 的代数式表示
的代数式表示![]() 为_____________;
为_____________;
②小红的“![]() 始终在
始终在![]() 的内部”的说法是正确的吗,为什么?
的内部”的说法是正确的吗,为什么?
(2)根据小华的叙述,写出![]() 与
与![]() 的数量关系并说明.
的数量关系并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一系列用同样规格的黑白两色正方形瓷砖铺设长方形地面.请观察并解答下列问题:
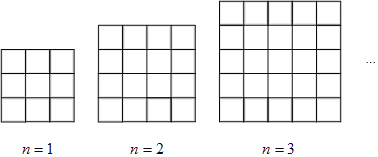
(1)在第n个图形中,共有多少块黑瓷砖(用含n的代数式表示);
(2)设铺设地面所用瓷砖的总块数为y,用(1)中的n表示y;
(3)当n=12时,求y的值;
(4)若黑瓷砖每块3元,白瓷砖每块2元,在问题(3)中,试求共需花多少元购买瓷砖.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元,已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次采购的数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.为出口需要,所有采购的大蒜必须在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半.为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com