|
|
|
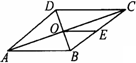
如图,在菱形ABCD中,对角线AC,BD相交于点O,E为BC的中点,则下列式子中一定成立的是
|
| [ ] |
A. |
AC=2OE
|
B. |
BC=2OE
|
C. |
AD=OE
|
D. |
OB=OE
|
|
|
练习册系列答案
相关习题
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
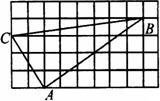
如图,若小方格边长为1,则△ABC是
|
| [ ] |
A. |
直角三角形
|
B. |
锐角三角形
|
C. |
钝角三角形
|
D. |
以上答案都不对
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
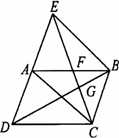
如图所示,已知在平行四边形ABCD中,E是边DA的延长线上一点,且AE=AD,连接EC,分别交AB、BD于点F、G,证明:AF=BF.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
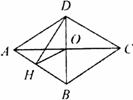
如图,四边形ABCD是菱形,对角线AC、BD相交于点O.DH⊥AB于点H,连接OH.求证:∠DHO=∠DCO.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
下列说法不正确的是
|
| [ ] |
A. |
有一个角是直角的菱形是正方形
|
B. |
两条对角线相等的菱形是正方形
|
C. |
对角线互相垂直的矩形是正方形
|
D. |
四条边都相等的四边形是正方形
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,正方形ABCD中,M是AB的中点,E是AB延长线上的一点,MN⊥DM,且交∠CBE的平分线于点N.
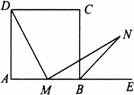
(1)求证:MD=MN.
(2)若将上述条件中的“M是AB的中点”改为“M是AB上的任一点”,其他条件不变,则结论“MD=MN”还成立吗?若成立,请证明;若不成立,请说明理由.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
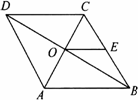
如图,在菱形ABCD中,对角线AC、BD交于点O,AB=8,E是BC的中点,则OE的长等于________.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,在□ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,给出下列结论:
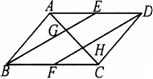
①△ABE≌△CDF;
②AG=GH=HC;
③ ; ;
④S△ABE=2S△AGB.其中正确的结论有________个.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如果△ABC的三边长分别为m2-1,2 m,m2+1,其中m为大于1的正整数,则
|
| [ ] |
A. |
△ABC是直角三角形,且斜边为m2-1
|
B. |
△ABC是直角三角形,且斜边为2 m
|
C. |
△ABC是直角三角形,且斜边为m2+1
|
D. |
△ABC不是直角三角形
|
|
|
查看答案和解析>>

 阅读快车系列答案
阅读快车系列答案