Question

5．如图，在平面直角坐标系中，已知点A坐标为（2，4），直线x=2与x轴相交于点B，抛物线y=x²的顶点在直线AO上运动，与直线x=2交于点P，设平移后的抛物线顶点M的横坐标为m．
（1）如图1，若m=-1，求点P的坐标；
（2）在抛物线平移的过程中，当△PMA是等腰三角形时，求m的值；
（3）如图2，当线段BP最短时，相应的抛物线上是否存在点Q，使△QMA的面积与△PMA的面积相等？若存在，请求出点Q的坐标；若不存在，请说明理由．

Answer 1

分析 （1）先求出直线OA的解析式，代入m=-1，求出抛物线的顶点坐标，即可求出抛物线解析式；
（2）过点M作MN垂直于直线x=2，过点P作PH⊥AM，连接MP，设出抛物线顶点坐标，表示PA，AM，MN，的长度，结合∠A的三角函数列出方程求解即可；
（3）先求出BP最短时的抛物线解析式，设出点Q坐标，根据题意构造平行线，分Q在直线OA的上方和下方两种情况分别列式求解即可．

解答 解：（1）设OA所在直线的函数解析式为y=kx，
∵A（2，4），
∴2k=4，
∴k=2，
∴OA所在直线的函数解析式为y=2x．
由题意，把x=-1，代入得，y=-2，
∴抛物线的顶点M（-1，-2），
∴抛物线解析式为：y=（x+1）²-2=x²+2x-1，
当x=2时，y=7，
∴点P（2，7）；
（2）如图1，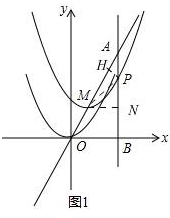

在抛物线平移的过程中，设顶点坐标（m，2m）当△PMA是等腰三角形时，
当PA=PM，
由点A（2，4），
可求：tan∠A=$\frac{1}{2}$，cos∠A=$\frac{2\sqrt{5}}{5}$，
过点M作MN垂直于直线x=2，过点P作PH⊥AM，连接MP，
抛物线解析式为：y=（x-m）²+2m，
当x=2时，y=m²-2m+4，
此时，MN=2-m，AN=4-2m，
AP=4-（m²-2m+4）=-m²+2m，
∴AH=AP×$\frac{2\sqrt{5}}{5}$=$\frac{-2\sqrt{5}{m}^{2}+4\sqrt{5}m}{5}$，
AM=2AH=$\frac{-4\sqrt{5}{m}^{2}+8\sqrt{5}m}{5}$，
∴$\frac{AN}{AM}$=$\frac{2\sqrt{5}}{5}$，
代入解得：m=$\frac{5}{4}$，或m=2（舍去）
∴m=$\frac{5}{4}$；
②昂AM=AP时，$\frac{-4\sqrt{5}{m}^{2}+8\sqrt{5}m}{5}$=-m²+2m，
解得：m=2或0，都不合题意舍弃，
③当MA=MP时，$\frac{\frac{1}{2}AP}{AM}$=cos∠A，
∴$\frac{1}{2}$（-m²+2m）=$\frac{2\sqrt{5}}{5}$•$\frac{-4\sqrt{5}{m}^{2}+8\sqrt{5}m}{5}$，
解得m=0或2不合题意舍弃
综上所述，m的值为$\frac{5}{4}$

（3）如图2，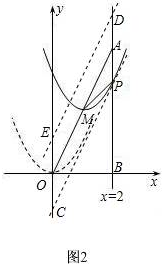

∵顶点M的横坐标为m，且在直线OA上移动，
∴y=2m．
∴顶点M的坐标为（m，2m）．
∴抛物线函数解析式为y=（x-m）²+2m．
∴当x=2时，y=（2-m）²+2m=m²-2m+4．
∴点P的坐标是（2，m²-2m+4）．
∵PB=m²-2m+4=（m-1）²+3，
∴当m=1时，PB最短．
当线段PB最短时，此时抛物线的解析式为y=（x-1）²+2
即y=x²-2x+3．
假设在抛物线上存在点Q，使S_△QMA=S_△PMA．
设点Q的坐标为（x，x²-2x+3）．
①点Q落在直线OA的下方时，过P作直线PC∥AO，交y轴于点C，
∵PB=3，AB=4，
∴AP=1，
∴OC=1，
∴C点的坐标是（0，-1），
∵点P的坐标是（2，3），
∴直线PC的函数解析式为y=2x-1，
∵S_△QMA=S_△PMA，
∴点Q落在直线y=2x-1上，
∴x²-2x+3=2x-1，
解得x₁=2，x₂=2，
即点Q（2，3），
∴点Q与点P重合，
∴此时抛物线上存在点Q（2，3），使△QMA与△APM的面积相等，
②当点Q落在直线OA的上方时，
作点P关于点A的对称称点D，过D作直线DE∥AO，交y轴于点E，
∵AP=1，
∴EO=DA=1，
∴E、D的坐标分别是（0，1），（2，5），
∴直线DE函数解析式为y=2x+1，
∵S_△QMA=S_△PMA，
∴点Q落在直线y=2x+1上，
∴x²-2x+3=2x+1，
解得：x=$2+\sqrt{2}$，或x=$2-\sqrt{2}$，
代入y=2x+1，得：y=$5+2\sqrt{2}$或y=$5-2\sqrt{2}$，
∴△QMA的面积与△PMA的面积相等时，点Q的坐标为：（$2+\sqrt{2}$，$5+2\sqrt{2}$），（$2-\sqrt{2}$，$5-2\sqrt{2}$）．

点评 本题考查二次函数的综合问题，题中涉及了一次函数解析式的确定、二次函数图象的平移、函数图象的交点、图形面积的求法等知识点，主要考查学生分类讨论和数形结合的数学思想方法．