
. |
| 13xy54 |
. |
| 13xy54 |
. |
| 13xy54 |
. |
| 13xy54 |
. |
| 13xy54 |
|
|
|


科目:初中数学 来源: 题型:
 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与函数y=
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与函数y=| k |
| x |
| 1 |
| 2 |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
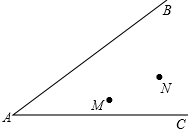 如图,两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且使PM=PN,请你通过尺规作图找出这一P点,(不写作法,保留作图痕迹).
如图,两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且使PM=PN,请你通过尺规作图找出这一P点,(不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:
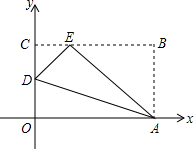 如图,OABC是一张放在平面直角坐标系中的长方形纸片.O为原点,OA=10,OC=8,在OC上取一点D,将纸片沿AD折叠使点O落在BC边上的点E处,则D、E的坐标分别是
如图,OABC是一张放在平面直角坐标系中的长方形纸片.O为原点,OA=10,OC=8,在OC上取一点D,将纸片沿AD折叠使点O落在BC边上的点E处,则D、E的坐标分别是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com