
【题目】如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为_______cm.

【答案】4.8;
【解析】
连接AP,先利用勾股定理的逆定理证明△ABC为直角三角形,∠BAC=90°,再证明四边形AEPF为矩形,则AP=EF,当AP的值最小时,EF的值最小,利用垂线段最短得到AP⊥BC时,AP的值最小,然后利用面积法计算此时AP的长即可.
解:
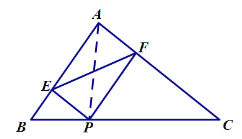
连接AP,
∵AB=6cm,AC=8cm,BC=10cm,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°,
又∵PE⊥AB,PF⊥AC,
∴四边形AEPF是矩形,
∴AP=EF,
当AP⊥BC时,EF的值最小,
SABC=![]() AB×AC=
AB×AC=![]() BC×AP
BC×AP
则:![]() ×6×8=
×6×8=![]() ×10×AP,
×10×AP,
解得AP=4.8cm.
∴EF的最小值是4.8cm.
答案为4.8.


科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
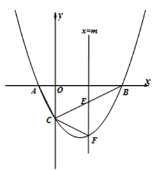
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=
与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=![]() x-2,作垂直于x轴的直线
x-2,作垂直于x轴的直线![]() ,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
(1)求抛物线的解析式;
(2)若△CEF是以CE为腰的等腰三角形,求m的值;
(3)点P为y轴左侧抛物线上的一点,过点P作![]() 交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
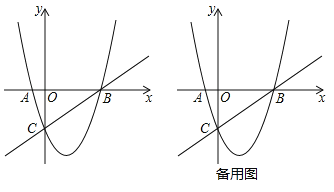
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() 与y轴交于点C,抛物线
与y轴交于点C,抛物线![]() 经过点B,C,与x轴的另一个交点为A.
经过点B,C,与x轴的另一个交点为A.
(1)求抛物线的解析式;
(2)点P是直线![]() 下方抛物线上一动点,求四边形
下方抛物线上一动点,求四边形![]() 面积最大时点P的坐标;
面积最大时点P的坐标;
(3)若M是抛物线上一点,且![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应垃圾分类处理,改善生态环境的号召,某小区将生活垃圾分成四类:厨余垃圾、可回收垃圾、不可回收垃圾、有害垃圾,分别记为a、b、c、![]() 并且设置了相应的垃圾箱:“厨余垃圾”箱,“可回收垃圾”箱,“不可回收垃圾”箱,“有害垃圾”箱,分别记为A,B,C,D.
并且设置了相应的垃圾箱:“厨余垃圾”箱,“可回收垃圾”箱,“不可回收垃圾”箱,“有害垃圾”箱,分别记为A,B,C,D.
![]() 如果将一袋有害垃圾任意投放进垃圾箱,则投放正确的概率是________.
如果将一袋有害垃圾任意投放进垃圾箱,则投放正确的概率是________.
![]() 小明将家里的厨余垃圾、可回收垃圾分装在两个袋中,任意投放在其中两个垃圾箱中,用画树状图或列表的方法求这两袋垃圾都投放正确的概率.
小明将家里的厨余垃圾、可回收垃圾分装在两个袋中,任意投放在其中两个垃圾箱中,用画树状图或列表的方法求这两袋垃圾都投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.
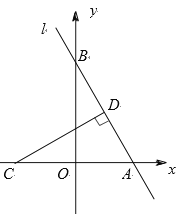
(1)求点D,O之间的距离;
(2)当tan∠CDO=![]() 时,求直线l的解析式;
时,求直线l的解析式;
(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设抛物线y=ax2+bx+c与x轴交于两个不同的点A(﹣1,0),B(m,0),与y轴交于点C(0,﹣2),且∠ACB=90度.
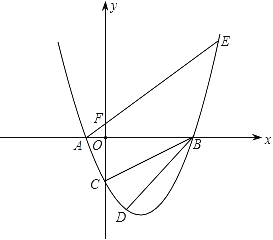
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E,求点D和点E的坐标;
(3)在x轴上是否存在点P,使以点P,B,D为顶点的三角形与三角形AEB相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
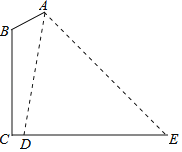
【题目】如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com