

分析 (1)先根据CB∥OA得出∠AOC+∠C=180°,故可得出∠COA的度数,再由角平分线的定义得出∠1=∠2,∠3=∠4.根据∠COA=∠1+∠2+∠3+∠4=60°可得出∠EOB的度数;
(2)根据BC∥OA可知∠5=∠FOA=∠3+∠4,∠6=∠4,再由∠3=∠4,可得出∠6=∠3,∠5-2∠6,即∠OFC=2∠OBC,故可得出结论;
(3)先求出∠COE1,探究规律后即可求解.
解答 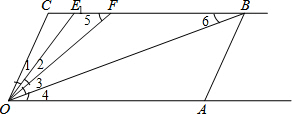 解:(1)∵CB∥OA,
解:(1)∵CB∥OA,
∴∠AOC+∠C=180°,∠6=∠4.
∵∠C=120°,
∴∠COA=60°.
∵OE1平分∠COF (已知),
∴∠1=∠2.
∵∠3=∠6,∠6=∠4,
∴∠3=∠4.
∵∠COA=∠1+∠2+∠3+∠4=60°,
∴∠2+∠3=$\frac{1}{2}$∠COA=30°,即∠E1OB=30°;
(2)∠OBC:∠OFC=1:2.
∵BC∥OA,
∴∠5=∠FOA=∠3+∠4,∠6=∠4(两直线平行,内错角相等).
又∵∠3=∠4,
∴∠6=∠3,
∴∠5-2∠6,即∠OFC=2∠OBC.
∴若向右平行移动AB,其它条件不变,那么∠OBC:∠OFC的值不发生变化;
(3)∵∠COE1=30°-x,OE2平分∠COE1,
∴∠COE2=$\frac{1}{2}$(30°-x),
∵OE3平分∠COE2,
∴∠COE3=$\frac{1}{4}$(30°-x),
∵OE4平分∠COE3,
∴∠COE4=$\frac{1}{8}$(30°-x).
∴∠OE4C=180°-120°-$\frac{1}{8}$(30°-x)=($\frac{225}{4}$)°+$\frac{1}{8}$x
点评 本题主要考查了平行线、角平分线的性质以及平行四边形的性质,有一定的综合性,难度适中.


科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )
如图,在?ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )| A. | 4 | B. | 3 | C. | $\frac{5}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.5×104米 | B. | 3.5×10-4米 | C. | 3.5×10-5米 | D. | 3.5×10-9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,?ABCD的对角线AC与BD相交于点O,E为CD边中点,BC=6cm,则OE的长为( )
如图,?ABCD的对角线AC与BD相交于点O,E为CD边中点,BC=6cm,则OE的长为( )| A. | 2cm | B. | 3cm | C. | $\sqrt{6}$cm | D. | 2$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平行四边形ABCD中,EF∥BC,AE:EB=2:3,EF=4,则AD的长为( )
如图,平行四边形ABCD中,EF∥BC,AE:EB=2:3,EF=4,则AD的长为( )| A. | $\frac{16}{3}$ | B. | 8 | C. | 10 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com