
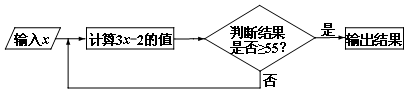
分析 (1)将x=8代入3x-2逐次判断是否大于55即可得;
(2)表示出第一次输出结果,根据“程序一次运算就输出结果”列不等式求解可得;
(3)表示出第一次、第二次、第三次的输出结果,再由第三次输出结果可得出不等式,解出即可.
解答 解:(1)当x=8时,3x-2=22<55,
当x=22时,3x-2=64>55,
故当输入实数x=8时,输出结果是64.
(2)第一次的结果为:3x-2,输出,则
3x-2≥55,
解得:x≥19.
故x的最小值是19;
(3)第一次的结果为:3x-2,没有输出,则3x-2<55,
解得:x<19;
第二次的结果为:3(3x-2)-2=9x-8,没有输出,则9x-8<55,
解得:x<7;
第三次的结果为:3(9x-8)-2=27x-26,输出,则27x-26≥55,
解得:x≥3;
综上可得:3≤x<7.
故整数x=3,4,5,6.
故答案为:64.
点评 本题考查了一元一次不等式的应用,解答本题的关键是读懂题意,根据结果是否可以输出,得出不等式.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:解答题
| 普通(元/间•天) | 豪华(元/间•天) | |
| 三人间 | 150 | 300 |
| 双人间 | 140 | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | 20 | D. | 16或20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 周末小明从家出发沿金牛山公园散步,经过篮球场地看了一会篮球赛,然后继续散步了一段时间,最后回到家中,如图描述了小明散步过程中离家的距离s(米)与散步时间t(分)间的关系,下列说法错误的是( )
周末小明从家出发沿金牛山公园散步,经过篮球场地看了一会篮球赛,然后继续散步了一段时间,最后回到家中,如图描述了小明散步过程中离家的距离s(米)与散步时间t(分)间的关系,下列说法错误的是( )| A. | 小明看篮球赛用时16分钟 | B. | 篮球场地距小明家600米 | ||
| C. | 小明离家最远距离为1200米 | D. | 小明从家出发到回家共用时32分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知等腰△ABC,AB=AC.
如图所示,已知等腰△ABC,AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com