
【题目】已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积.

【答案】84
【解析】首先连接BD,再利用勾股定理计算出BD的长,再根据勾股定理逆定理计算出∠D=90°,然后计算出直角三角形ABD和直角三角形BDC的面积,即可算出答案.
解:连接BD,
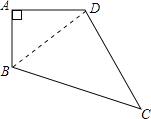
∵∠A=90°,AB=3cm,AD=4cm,
∴BD=![]() =
=![]() =5(cm),
=5(cm),
∵52+122=132,
∴BD2+CD2=CB2,
∴∠BDC=90°,
∴S△DBC=![]() ×DB×CD=
×DB×CD=![]() ×5×12=30(cm2),
×5×12=30(cm2),
S△ABD=![]() ×3×4=6(cm2),
×3×4=6(cm2),
∴四边形ABCD的面积为30+6=36(cm2),
故答案为:36(cm2).
“点睛”此题主要考查了勾股定理,以及勾股定理的逆定理,解决此题的关键是算出BD的长,△BDC是直角三角形.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 有理数是指整数、分数、零、正有理数、负有理数这五类
B. 一个有理数不是正数就是负数
C. 一个有理数不是整数就是分数
D. 以上说法都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面一组按规律排列的数:1, 2,4, 8,16,……,第2002个数应是( )
A. 22002 B. 22002-1 C. 22001 D. 以上答案不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个
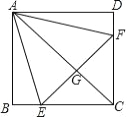
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产A、B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图.

并求得了A产品三次单价的平均数和方差:
A=5.9;s2A=[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]= .
(1)补全图中B产品单价变化的折线图. B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片,卡片除颜色和数字外其它完全相同.
(1)从中任意抽取一张卡片,则该卡片上写有数字1的概率是 ;
(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率.(请利用树状图或列表法说明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com