练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．若$\frac{4x-9}{（3x+2）（x-1）}$=$\frac{A}{3x+2}$-$\frac{B}{x-1}$（A、B为常数），则A•B的值为7．

    分析 通过通分得到分子的对应项，从而求得A、B的值，则易求A•B的值．

    解答 解：∵$\frac{A}{3x+2}$-$\frac{B}{x-1}$=$\frac{（x-1）A-（3x+2）B}{（3x+2）（x-1）}$=$\frac{（A-3B）x-（A+2B）}{（3x+2）（x-1）}$，
    ∴$\frac{4x-9}{（3x+2）（x-1）}$=$\frac{（A-3B）x-（A+2B）}{（3x+2）（x-1）}$，
    ∴$\left\{\begin{array}{l}{A-3B=4}\\{A+2B=9}\end{array}\right.$，
    解得$\left\{\begin{array}{l}{A=7}\\{B=1}\end{array}\right.$，
    ∴A•B=7×1=7．
    故答案是：7．

    点评 本题考查了分式的加减法，先通分，然后进行同分母分式加减运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．已知关于x，y的二元一次方程组$\left\{\begin{array}{l}ax+4y=2\\ 7x-by=-3\end{array}$的解是$\left\{\begin{array}{l}x=1\\ y=2.\end{array}$，求（a+b）2016的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．已知∠A=30°，则这个角的余角是（　　）
    A．30°B．60°C．90°D．150°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．若一个多边形的每一个外角都等于36度，求这个多边形的内角和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．解方程：
    （1）x（2x-5）=4x-10    
    （2）2x2-x-1=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．若点P（x，-4）与点Q（3，y）关于原点对称，则x-y等于（　　）
    A．1B．-1C．-7D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

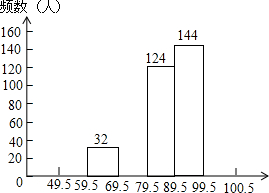    15．某市九年级有15000名学生参加学业水品测试，为了了解本次测试的成绩分布情况，从中抽取了400名学生的得分（得分取正整数，满分100分）进行统计：
    频 率 分 布 表
    分  组频  数频  率
    49.5～59.5200.05
    59.5～69.5320.08
    69.5～79.5800.20
    79.5～89.51240.31
    89.5～100.51440.36
    合  计4001
    请你根据不完整的频率分布表，解答下列问题：
    （1）补全频率分布表和频数分布直方图；
    （2）若将得分转化为等级，规定得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”，这15000名学生中约有多少人为“D”？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．在数-5，1，3，5，-2中，任取三个数相乘，所得积的绝对值最大是75．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．给出下列数：-18，$\frac{22}{7}$，3.1416，0，2001，-$\frac{3π}{5}$，-0.14，95%，其中负数有-18，-$\frac{3π}{5}$，-0.14，整数有-18，0，2001，负分数有-0.14．

    查看答案和解析>>

    同步练习册答案