
【题目】如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5㎝,AB= ![]() ㎝,则劣弧
㎝,则劣弧 ![]() 与AB,AP所围成的阴影的面积是.
与AB,AP所围成的阴影的面积是.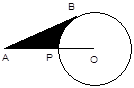
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作角的平分线”的尺规作图的过程.
已知:如图1,![]() .
.
求作:射线![]() ,使它平分
,使它平分![]() .
.
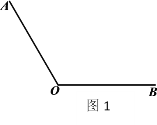
作法:如图2,
①以点![]() 为圆心,任意长为半径作弧,交
为圆心,任意长为半径作弧,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;
;
②分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的同样长为半径作弧,两弧交于点
的同样长为半径作弧,两弧交于点![]() ;
;
③作射线![]() .
.
所以射线![]() 就是所求作的射线.
就是所求作的射线.
根据小明设计的尺规作图的过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接![]() ,
,![]() .
.
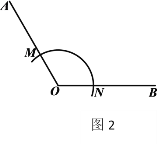
在![]() 和
和![]() 中,
中,
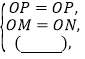
∴![]() ≌
≌![]() ( )(填推理的依据).
( )(填推理的依据).
∴ (全等三角形的 相等).
即射线![]() 平分
平分![]() (角平分线定义).
(角平分线定义).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来数的情况下,为估计白球数,小刚向其中放入8个黑球摇匀后,从中随意摸出一个球记下颜色,再把它放回盒中,不断重复这一过程,共摸球100次,其中20次摸到黑球,你估计盒中大约有白球( )
A.20个
B.28个
C.36个
D.32个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )
A.π
B.![]()
![]() π
π
C.![]() π
π
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a2﹣ab+b2)﹣(3a2+ab+b2),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+![]() a2)+(3b+
a2)+(3b+![]() a2)+…+(9b+
a2)+…+(9b+![]() a2)的值.
a2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下面的问题:
(1)如果a2+a=3,求a2+a+2015的值.
(2)已知a﹣b=﹣3,求3(b﹣a)2﹣5a+5b+5的值.
(3)已知a2+2ab=﹣3,ab﹣b2=﹣5,求4a2+![]() ab+
ab+![]() b2的值.
b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB于点E,F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其他条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB和直线BC于E、F和G. 试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8.

(1)用直尺和圆规作∠A的平分线,交BC于点D;(要求:不写作法,保留作图痕迹)
(2)SADC:SADB .(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com