
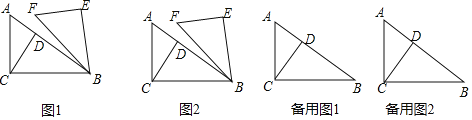
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点D,将
于点D,将![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() 得到
得到![]()
![]() 如图2,当
如图2,当![]() 时,求点C、E之间的距离;
时,求点C、E之间的距离;
![]() 在旋转过程中,当点A、E、F三点共线时,求AF的长;
在旋转过程中,当点A、E、F三点共线时,求AF的长;
![]() 连结AF,记AF的中点为P,请直接写出线段CP长度的最小值.
连结AF,记AF的中点为P,请直接写出线段CP长度的最小值.
【答案】(1)CE=![]() ;(2)AF的长为
;(2)AF的长为![]() +
+![]() 或
或![]() ﹣
﹣![]() ;(3)CP的最小值=OC﹣OP=2﹣
;(3)CP的最小值=OC﹣OP=2﹣![]() .
.
【解析】
(1)只要证明∠CBE=90°,求出BE,BC利用勾股定理即可解决问题.
(2)分两种情形画出图形分别求解即可.
(3)如图3中,取AB的中点O,连接OP,CO.利用三角形的中位线定理可得OP=![]() ,推出点P的运动轨迹是以O为圆心
,推出点P的运动轨迹是以O为圆心![]() 为半径的圆,由此即可解决问题.
为半径的圆,由此即可解决问题.
解:(1)如图1中,
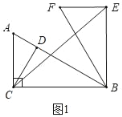
在Rt△ABC中,∵∠ACB=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,BC=![]() =2
=2![]() ,
,
∵CD⊥AB,
∴![]() ABCD=
ABCD=![]() ACBC,
ACBC,
∴CD=![]() =
=![]() =
=![]() ,
,
∴BD=BE=![]() =3,
=3,
∵∠ABE=α=60°,
∴∠CBE=30°+60°=90°,
∴CE=![]() =
=![]() =
=![]() .
.
(2span>)如图2﹣1中,

∵A,F,E三点共线,
∴∠AEB=90°,AE=![]() =
=![]() =
=![]() ,
,
∴AF=AE﹣EF=![]() ﹣
﹣![]() .
.
如图2﹣2中,
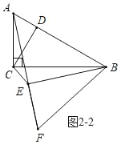
当A,E,F共线时,∠AEB=90°,AE=![]() =
=![]() =
=![]() ,
,
∴AF=AE+EF=![]() +
+![]() .
.
综上所述,AF的长为![]() +
+![]() 或
或![]() ﹣
﹣![]() .
.
(3)如图3中,取AB的中点O,连接OP,CO.

∵AO=OB,AP=PF,
∴OP=![]() BF=
BF=![]() BC=
BC=![]() ,
,
∴点P的运动轨迹是以O为圆心![]() 为半径的圆,
为半径的圆,
∵OC=![]() AB=2,
AB=2,
∴CP的最小值=OC﹣OP=2﹣![]() .
.
故答案为:(1)CE=![]() ;(2)AF的长为
;(2)AF的长为![]() +
+![]() 或
或![]() ﹣
﹣![]() ;(3)CP的最小值=OC﹣OP=2﹣
;(3)CP的最小值=OC﹣OP=2﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是( )
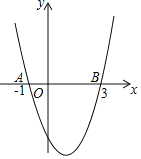
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小红家阳台上放置了一个晒衣架.如图2是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条直线,且EF=32cm.(参考数据:sin61.9°≈0.882,cos61.9°≈0.471,tan28.1°≈0.534)
(1)求证:AC∥BD;
(2)求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°);
(3)小红的连衣裙穿在衣架后的总长度达到122cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量瀑布AB的高度,测量人员在瀑布对面山上的D点处测得瀑布顶端A点的仰角是![]() ,测得瀑布底端B点的俯角是
,测得瀑布底端B点的俯角是![]() ,AB与水平面垂直
,AB与水平面垂直![]() 又在瀑布下的水平面测得
又在瀑布下的水平面测得![]() ,
,![]() 注:C、G、F三点在同一直线上,
注:C、G、F三点在同一直线上,![]() 于点
于点![]() ,斜坡
,斜坡![]() ,坡角
,坡角![]() (参考数据:
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
![]() 求测量点D距瀑布AB的距离
求测量点D距瀑布AB的距离![]() 精确到
精确到![]() ;
;
![]() 求瀑布AB的高度
求瀑布AB的高度![]() 精确到
精确到![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
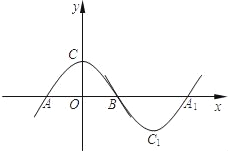
【题目】如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
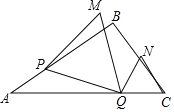
【题目】如图,在△ABC中,AB=7.5,AC=9,S△ABC=![]() .动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
.动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
(1)求cosA的值;
(2)当△PQM与△QCN的面积满足S△PQM=![]() S△QCN时,求t的值;
S△QCN时,求t的值;
(3)当t为何值时,△PQM的某个顶点(Q点除外)落在△QCN的边上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦前夕,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人小丁第![]() 天生产的粽子数量为
天生产的粽子数量为![]() 只,
只,![]() 与
与![]() 满足如下关系:
满足如下关系:![]()
(1)小丁第几天生产的粽子数量为280只?
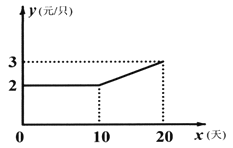
(2)如图,设第![]() 天生产的每只粽子的成本是
天生产的每只粽子的成本是![]() 元,
元,![]() 与
与![]() 之间的关系可用图中的函数图象来刻画.若小丁第
之间的关系可用图中的函数图象来刻画.若小丁第![]() 天创造的利润为
天创造的利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com