

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
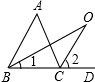 解:(1)探究2结论:∠BOC=
解:(1)探究2结论:∠BOC=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2015届江苏省扬州市邗江区七年级下学期期末考试数学试卷(解析版) 题型:解答题
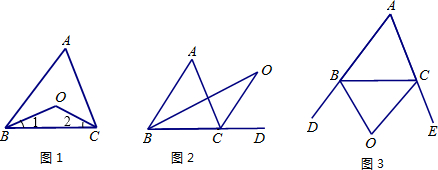
认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.

探究1:如图1,在 中,
中, 是
是 与
与 的平分线
的平分线 和
和 的交点,分析发现
的交点,分析发现 ,理由如下: ∵
,理由如下: ∵ 和
和 分别是
分别是 ,
, 的角平分线
的角平分线



(1)探究2:如图2中,  是
是 与外角
与外角 的平分线
的平分线 和
和 的交点,试分析
的交点,试分析 与
与 有怎样的关系?请说明理由.
有怎样的关系?请说明理由.
(2)探究3: 如图3中, 是外角
是外角 与外角
与外角 的平分线
的平分线 和
和 的交点,则
的交点,则 与
与 有怎样的关系?(直接写出结论)
有怎样的关系?(直接写出结论)
(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)
(4)运用:如图5,五边形ABCDE中,∠BCD、∠EDC的外角分别是∠FCD、∠GDC,CP、DP分别平分∠FCD和∠GDC且相交于点P,若∠A=140°,∠B=120°,∠E=90°,则∠CPD=_____度.
查看答案和解析>>
科目:初中数学 来源:2012年北京石景山区中考模拟数学卷 题型:解答题
认真阅读下面关于三角形内外角平分线所夹的探究片段,完成所提出的问题.
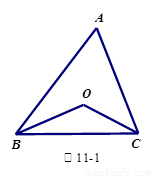
探究如图11-1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+ ,理由如下:
,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
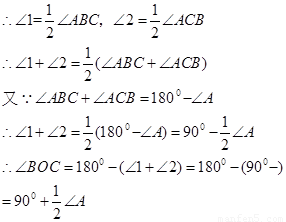
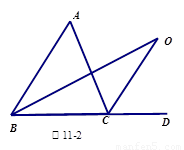
1.如图11-2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
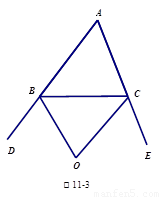
2.如图11-3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
结论: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com