
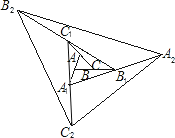
【题目】如图,Rt△ABC中,∠ACB=90°,点M为BA延长线上一点,∠ABC的平分线BE和∠CAM的平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G,则下列结论:①∠APB=45°;②PF=PA;③DG=AP+GH;④BD﹣AH=AB.其中正确的是_____(填序号).

【答案】①②④
【解析】
①正确.证明∠APB=![]() ∠ACB即可.
∠ACB即可.
②正确.证明△PBA≌△PBF(ASA)即可.
③错误.证明DG=AG,GH=GF,AF>AP即可判断.
④正确.根据BD﹣AH=BD﹣DF=BF=AB可得结论.
解:由题意可以假设∠MAP=∠PAC=x,∠ABP=∠PBD=y,
则有![]() ,
,
可得∠APB=![]() ∠ACB=45°,故①正确,
∠ACB=45°,故①正确,
∵PF⊥AD,
∴∠APF=90°,
∴∠APB=∠FPB=45°,
∵PB=PB,∠ABP=∠PBF,
∴△PBA≌△PBF(ASA),
∴PA=PF,BA=BF,故②正确,
∵HP⊥AD,DC⊥AH,
∴AG⊥DH,
∵∠DPF=∠HCF=90°,∠DFP=∠HFC,
∴∠PDF=∠PHA,
∵∠DPF=∠APH=90°,PF=PA,
∴△DPF≌△HPA(AAS),
∴DF=AH,PD=PH,
∴∠PDH=∠AHP=45°,
∴∠ADG=∠DAG=45°,
∴DG=AG,
∵∠GHF=∠GFH=45°,
∴GH=FG,
∵DG=FG+AH=GH+AF,AF>PA,
∴DG≠GH+PA,故③错误,
∵BD﹣AH=BD﹣DF=BF,BF=AB,
∴BD﹣AH=AB,故④正确.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】计算题:
(1)(﹣1)23×(π﹣3)0﹣(﹣![]() ) ﹣3;
) ﹣3;
(2)aa2a3+(﹣2a3)2﹣a8÷a2;
(3)(x+4)2﹣(x+2)(x﹣2);
(4)(a+2b﹣3c)(a﹣2b+3c).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个正整数m,如果m=k(k+1),其中k是正整数,则称m为“矩数”,k 为m的最佳拆分点.例如,56=7×(7+1),则56是一个“矩数”,7为56的最佳拆分点.
(1)求证:若“矩数”m是3的倍数,则m一定是6的倍数;
(2)把“矩数”p与“矩数”q的差记为 D(p,q),其中p>q,D(p,q)>0.例如,20=4×5,6=2×3,则 D(20,6)=20﹣6=14.若“矩数”p的最佳拆分点为t,“矩数”q的最佳拆分点为s,当 D(p,q)=30时,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2019,最少经过( )次操作.
A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,右边数位上的数总比左边数位上的数大1,则我们称这样的自然数叫“美数”,例如:123,3456,67,…都是“美数”.
(1)若某个三位“美数”恰好等于其个位的76倍,这个“美数”为 .
(2)证明:任意一个四位“美数”减去任意一个两位“美数”之差再减去1得到的结果定能被11整除;
(3)如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上的数大1,则我们称这样的自然数叫“妙数”,若任意一个十位为![]()
![]() 为整数)的两位“妙数”和任意一个个位为
为整数)的两位“妙数”和任意一个个位为![]() 为整数)的两位“美数”之和为55,则称两位数
为整数)的两位“美数”之和为55,则称两位数![]() 为“美妙数”,并把这个“美妙数”记为
为“美妙数”,并把这个“美妙数”记为![]() ,则求
,则求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
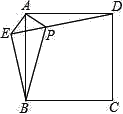
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距50千米.星期天上午8:00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程y(千米)与小聪行驶的时间x(小时)之间的函数关系如图所示,小明父亲出发小时时,行进中的两车相距8千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空.如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD,理由如下:
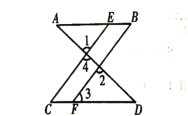
解:因为∠1=∠2(已知),且∠1=∠4( )
所以∠2=∠4(等量代换)
所以CE∥BF( )
所以∠ =∠3( )
又因为∠B=∠C(已知),所以∠3=∠B( )
所以AB∥CD ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com