
 ����ij��ԭ����һ����ֱ�Ĺ�·���ڽ�����·���40ǧ��A��B���أ��ֱ��мס�������ҽ��վ����ͼ����A�ر�ƫ��45�㣬B�ر�ƫ��60�㷽������һ������C������C��CH��AB��H��
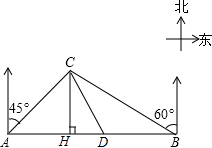
����ij��ԭ����һ����ֱ�Ĺ�·���ڽ�����·���40ǧ��A��B���أ��ֱ��мס�������ҽ��վ����ͼ����A�ر�ƫ��45�㣬B�ر�ƫ��60�㷽������һ������C������C��CH��AB��H������ ��1����CH=x���ֱ��ʾ��AH��BH��ֵ��������ӵ�40��ֵ�������CH�ij������������CB�ij���
��2����CD��BC��������ϵ�ɵ�CD��CH��������ϵ����������ǵ����Ǻ���ֵ�������ADC�Ķ����������ɵ�HD�ij�����BH�ij���ȥDH�ij���ΪBD�ľ��룮
��� �⣺��1����CHΪxǧ�ף�������ã���CBH=30�㣬��CAH=45�㣬
��AH=CH=x��
��Rt��BCH��tan30��=$\frac{x}{BH}$=$\frac{\sqrt{3}}{3}$��
��BH=$\sqrt{3}$x��
��AH+HB=AB=40��
��x+$\sqrt{3}$x=40��
���x=20$\sqrt{3}$-20��
��CB=2CH=40$\sqrt{3}$-40��
��������C��B�صľ���Ϊ��40$\sqrt{3}$-40��ǧ�ף�
��2����C��D ���ؾ�����B��C���ؾ����$\frac{\sqrt{3}}{3}$����CH=$\frac{1}{2}$BC��
��sin��ADC=$\frac{CH}{CD}$=$\frac{\frac{1}{2}BC}{\frac{\sqrt{3}}{3}BC}$=$\frac{\sqrt{3}}{2}$��
���ADC=60�㣮
��Rt��CHD�У�DH=CH•cot��CDH=$\frac{\sqrt{3}}{3}$CH��
��BH=$\sqrt{3}$CH��CH=20$\sqrt{3}$-20��
��BD=BH-DH=$\sqrt{3}$CH-$\frac{\sqrt{3}}{3}$CH=$\frac{2\sqrt{3}}{3}$��20$\sqrt{3}$-20��=40-$\frac{40\sqrt{3}}{3}$��
��BD֮��ľ���Ϊ40-$\frac{40\sqrt{3}}{3}$ǧ�ף�
���� ���⿼���˽�ֱ�������ε�Ӧ���Լ�����ֱ�������Σ����ù��ɶ�������������Ǻ���ֵ����ǽ������ؼ���


 һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д� ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
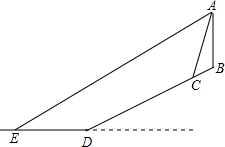 �п�������С���ͺ�����һ��ǰ���������Σ�������ס�ı���AB�������¶�Ϊi=1��2.4��б���ϣ�ij�죬С���ڱ��ݶ�¥�ĺ�����A�����⿴�羰�����ֱ���ǰ�� һ������C�ĸ���Ϊ76�㣨����ĸ߶Ⱥ��Բ��ƣ���Զ��������һ�Ҽ����������ִ�E�ĸ���Ϊ27�㣮��֪����C���뺣����D�ľ���CDΪ260�ף������AB��ˮƽ����Ϊ36�ף��ʴ�ʱ�ִ�E���뺣����D�ľ���ED�ij�Ϊ�����������ο����ݣ�tan76���4.0��tan27���0.5��sin76���0.97��sin27���0.45��
�п�������С���ͺ�����һ��ǰ���������Σ�������ס�ı���AB�������¶�Ϊi=1��2.4��б���ϣ�ij�죬С���ڱ��ݶ�¥�ĺ�����A�����⿴�羰�����ֱ���ǰ�� һ������C�ĸ���Ϊ76�㣨����ĸ߶Ⱥ��Բ��ƣ���Զ��������һ�Ҽ����������ִ�E�ĸ���Ϊ27�㣮��֪����C���뺣����D�ľ���CDΪ260�ף������AB��ˮƽ����Ϊ36�ף��ʴ�ʱ�ִ�E���뺣����D�ľ���ED�ij�Ϊ�����������ο����ݣ�tan76���4.0��tan27���0.5��sin76���0.97��sin27���0.45��| A�� | 262 | B�� | 212 | C�� | 244 | D�� | 276 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
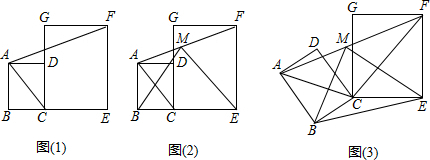
 ��ͼ���߶�AB�߳�Ϊ1����λ���ȵ������ηָ�Ϊ��������ֱ�������Σ���AΪԲ�ģ�AB�ij�Ϊ�뾶�����������ڵ�C����ô��C�������ϱ�ʾ��ʵ���ǣ�������
��ͼ���߶�AB�߳�Ϊ1����λ���ȵ������ηָ�Ϊ��������ֱ�������Σ���AΪԲ�ģ�AB�ij�Ϊ�뾶�����������ڵ�C����ô��C�������ϱ�ʾ��ʵ���ǣ�������| A�� | 1+$\sqrt{2}$ | B�� | $\sqrt{2}$ | C�� | $\sqrt{2}-1$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $m��\frac{1}{2}$ | B�� | m��1 | C�� | $m��-\frac{1}{2}$��m��1 | D�� | $-\frac{1}{2}��m��1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���Ķ�������������⣬�ٰ�Ҫ�����������⣺
���Ķ�������������⣬�ٰ�Ҫ�����������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com