
分析 根据圆内接正方形和正六边形的性质,将问题转化为关于三角形的问题,即可求出正方形和正六边形的边长,进而求出边长之比.
解答 解:如图1,在圆内接正方形ABCD中,OA=OD=R,∠AOD=360°×$\frac{1}{4}$=90°,
则内接正方形的边长为$\frac{R}{sin45°}$=$\sqrt{2}$R;
如图2,在圆内接正六边形ABCDEF中,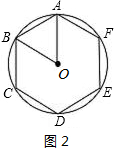
∠AOB=60°,
△AOB为正三角形,
则内接正六边形的边长为R,
所以其比为$\sqrt{2}$:1.
故答案为$\sqrt{2}$:1.
点评 本题考查了正多边形和圆,掌握基本的图形变换.找出内接正方形与外切正六边形的边长关系,是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,直角三角形ABE,∠AEB=90°,∠BAE=30°,以AB为边作菱形ABCD,∠DAB=60°,点Q从A出发,沿折线AD-DC运动,运动到点C停止,设点Q运动的时间为t(s).△AEQ的面积s(cm2)与t(s)之间函数关系的图象由图2中的线段OP、PF给出.
如图1,直角三角形ABE,∠AEB=90°,∠BAE=30°,以AB为边作菱形ABCD,∠DAB=60°,点Q从A出发,沿折线AD-DC运动,运动到点C停止,设点Q运动的时间为t(s).△AEQ的面积s(cm2)与t(s)之间函数关系的图象由图2中的线段OP、PF给出.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com