练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．若式子$\sqrt{2x+1}$在实数范围内有意义，则x的取值范围是（　　）
    A．x$≤-\frac{1}{2}$B．x$≥-\frac{1}{2}$C．x$＜-\frac{1}{2}$D．x$＞-\frac{1}{2}$

    分析 根据二次根式中的被开方数必须是非负数列出不等式，解不等式即可．

    解答 解：由题意得，2x+1≥0，
    解得，x≥-$\frac{1}{2}$，
    故选：B．

    点评 本题考查的是二次根式有意义的条件，掌握二次根式中的被开方数必须是非负数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    12．若一次函数y=x+m的图象经过第一、二、三象限，写出一个符合条件的m的值为1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列图形中既是轴对称图形又是中心对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．若?ABCD的三条边分别为8cm，（x-2）cm，（x+3）cm，则该?ABCD的周长是22或42cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

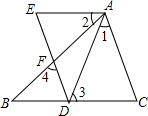    17．完成证明，说明理由．
    已知：如图，点D在BC边上，DE、AB交于点F，AC∥DE，∠1=∠2，∠3=∠4．
    求证：AE∥BC．
    证明：∵AC∥DE（已知），
    ∴∠4=∠FAC（两直线平行，同位角相等　）
    ∵∠3=∠4（已知），
    ∴∠3=∠FAC（等量代换　）
    ∵∠1=∠2（已知），
    ∴∠1+∠FAD=∠2+∠FAD（等式的性质）
    即∠FAC=∠EAD，
    ∴∠3=∠EAD．
    ∴AE∥BC（内错角相等，两直线平行　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

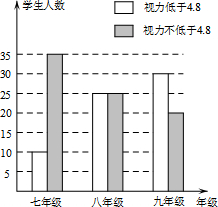    7．在学习了“普查与抽样调查”之后，某校八（1）班数学兴趣小组对该校学生的视力情况进行了抽样调查，并画出了如图所示的条形统计图．请根据图中信息解决下列问题：
    （1）本次抽查活动中共抽查了145名学生；
    （2）已知该校七年级、八年级、九年级学生数分别为360人、400人、540人．
    ①估算：该校九年级视力不低于4.8的学生约有216名；
    ②为了估算出该校视力低于4.8的学生数，小明是这样计算的：
    步骤一：计算样本中视力低于4.8的学生比例：
    $\frac{10+25+30}{（10+35）+（25+25）+（30+20）}$×100%≈44.83%．
    步骤二：用样本估计总体，从而求得全校视力低于4.8的学生数：
    （360+400+540）×44.83%≈583（名）．
    请你判断小明的估算方法是否正确？如果正确，请你计算出扇形统计图中“视力低于4.8”的圆心角的度数；如果不正确，请你帮忙估算出该校视力低于4.8的学生数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．在一个不透明布袋里面装有11个球，其中有4个红球，7个白球，每个球除颜色外其他完全相同，从中任意摸出一个球，是白球的概率是$\frac{7}{11}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．在一个不透明的袋子中装有三张分别标有1、2、3数字的卡片（卡片除数字外完全相同）．
    （1）从袋中任意抽取一张卡片，则抽出的是偶数的概率为$\frac{1}{3}$；
    （2）从袋中任意抽取二张卡片，求被抽取的两张卡片构成两位数是奇数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

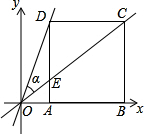    12．边长为2的正方形ABCD在平面直角坐标系中如图放置，已知点A的横坐标为1，作直线OC与边AD交于点E．
    （1）求点C的坐标；
    （2）过O，D两点作直线，记该直线与直线OC的夹角为α，试求tanα的值．

    查看答案和解析>>

    同步练习册答案