
 ,并且每两个小圆的公共部分的面积都小于
,并且每两个小圆的公共部分的面积都小于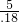 π?请说出你的结论,并给出证明.
π?请说出你的结论,并给出证明.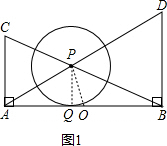 解:(1)如图1,连接PQ,
解:(1)如图1,连接PQ,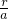 =
=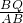 ,
, =
=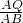
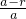 =
=
 ;
;
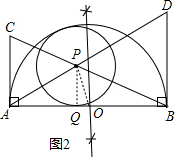
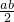
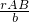 =
=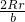 =a
=a -a=
-a=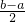
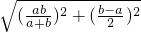 =
=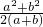 =
= -
- =R-r
=R-r =3,
=3, π,又设每个小圆的面积为S,三个小圆公共部分的面积为SPMN,则三个小圆的覆盖面积=3S-(SPM+SMN+SPN)+SPMN>3π•(
π,又设每个小圆的面积为S,三个小圆公共部分的面积为SPMN,则三个小圆的覆盖面积=3S-(SPM+SMN+SPN)+SPMN>3π•( )2-
)2-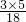 π+SPMN≥
π+SPMN≥ π=
π=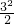 π=半圆O的面积,而这是不可能的,故不能在这个半圆O中画出符合要求的⊙M和⊙N.
π=半圆O的面积,而这是不可能的,故不能在这个半圆O中画出符合要求的⊙M和⊙N.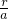 =
=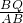 ,
, =
=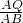 ,故可求得r的值;
,故可求得r的值; ,⊙P的半径为r=
,⊙P的半径为r= ,可得到AQ=
,可得到AQ=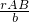 =
=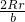 =a,OQ=
=a,OQ= -a=
-a=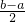 ,连接PO,由勾股定理得到PO=R-r,故⊙O与⊙P相切;
,连接PO,由勾股定理得到PO=R-r,故⊙O与⊙P相切;

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com