
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
利用交点式写出抛物线解析式为y=ax2﹣2ax﹣3a,配成顶点式得y=a(x﹣1)2﹣4a,则可对①进行判断;计算x=4时,y= a×5×1=5a,则根据二次函数的性质可对②进行判断;利用对称性和二次函数的性质可对③进行判断;由于b=﹣2a,c=﹣3a,则方程cx2+bx+a=0化为﹣3ax2﹣2ax+a=0,然后解方程可对④进行判断.
由二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0),
可得抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∵y=a(x﹣1)2﹣4a,
∴当x=1时,二次函数有最小值﹣4a,所以①正确;
当x=4时,y=a×5×1=5a,
∴当﹣1≤x2≤4,则﹣4a≤y2≤5a,所以②错误;
∵点C(1,5a)关于直线x=1的对称点为(﹣2,﹣5a),
∴当y2>y1,则x2>4或x<﹣2,所以③错误;
∵b=﹣2a,c=﹣3a,
∴方程cx2+bx+a=0化为﹣3ax2﹣2ax+a=0,
整理得3x2+2x﹣1=0,解得x1=﹣1,x2=![]() ,所以④正确,
,所以④正确,
故选B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校九年级举行毕业典礼,需要从九(1)班的2名男生1名女生、九(2)的1名男生1名女生共5人中选出2名主持人.
(1)用树形图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20 m和11 m的矩形大厅内修建一个60 m2的矩形健身房ABCD.该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/m2,新建(含装修)墙壁的费用为80元/m2.设健身房的高为3 m,一面旧墙壁AB的长为x m,修建健身房墙壁的总投入为y元.
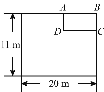
(1)求y与x的函数关系式;
(2)为了合理利用大厅,要求自变量x必须满足条件:8≤x≤12,当投入的资金为4800元时,问利用旧墙壁的总长度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民王先生上周星期五买进某公司股票1000股,每股18元,本周该股票的涨跌情况如表(正数表示价格比前一天上涨,负数表示价格比前一天下跌,单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
(1)星期三结束时,该股票每股多少元?
(2)该股票本周内每股的最高价和最低价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】路桥方林汽车城某4S店销售某种型号的汽车,每辆车的进货价为15万元,市场调研表明:当销售价为21万元时,平均每周能售出6辆,而当销售价每降低0.5万元时,平均每周能多售出3辆,如果设每辆汽车降价x万元,平均每周的销售利润为W万元
(1)该4S店要想平均周获得72万元的销售利润,并且要尽可能地让利于顾客,则每辆汽车的定价应为多少万元?
(2)试写出W与x之间的函数关系式,并说明当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线![]() 与该圆所围成的阴影部分(不包括边界)的整点个数是( )
与该圆所围成的阴影部分(不包括边界)的整点个数是( )

A. 24 B. 23 C. 22 D. 21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请解答下列各题:
(1)数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 之间的距离表示为_______,如果
之间的距离表示为_______,如果![]() ,那么
,那么![]() _______.
_______.
(2)若点![]() 表示的整数为
表示的整数为![]() ,则当
,则当![]() ________时,
________时,![]() .
.
(3)要使![]() 取最小值时,相应的
取最小值时,相应的![]() 的取值范围是________,最小值是________.
的取值范围是________,最小值是________.
(4)已知![]() ,则
,则![]() 的最大值为_______,最小值为_______.
的最大值为_______,最小值为_______.
(5)若![]() ,则
,则![]() 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为圆
为圆![]() 的直径,
的直径,![]() 为圆
为圆![]() 上一点,
上一点,![]() 为
为![]() 延长线一点,且
延长线一点,且![]() ,
,![]() 于点
于点![]() .
.
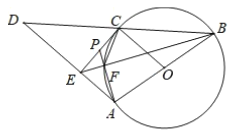
(1)求证:直线![]() 为圆
为圆![]() 的切线;
的切线;
(2)设![]() 与圆
与圆![]() 交于点
交于点![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,
,
①求证:![]()
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com