练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情


    如图6，从镜子中看到一钟表的时针和分针，此时的实际时刻是________．
    9：30
    从镜子里看到的钟表和原来的钟表轴对称的关系,如下图所示。所以此时的实际时间是9:30.（记得以后做这样的题目时，从卷子的背面就可以看到答案了）
    ，
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    （6分）如图，小芳和小丽想测量学校旗杆的高度，她们来到操场，小芳测得小丽身高1.6米，在阳光下的影子长度为2.4米，她想立刻测量旗杆的影长时，因旗杆靠近一教学楼，影子不全落在地面上，有一部分落在墙上，测得落在地面上影长为12米，留在墙上的影高为2米，求旗杆的高度.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    阅读下列材料，并解决后面的问题：
    ★阅读材料：
    (1) 等高线概念：在地图上，我们把地面上海拔高度相同的点连成的闭合曲线叫等高线。
    例如，如图1，把海拔高度是50米、100米、150米的点分别连接起来，就分别形成50米、100米、150米三条等高线。
    (2) 利用等高线地形图求坡度的步骤如下：(如图2)
    步骤一：根据两点A、B所在的等高线地形图，分别读出点A、B的高度；A、B两点
    的铅直距离=点A、B的高度差；
    步骤二：量出AB在等高线地形图上的距离为d个单位，若等高线地形图的比例尺为
    1：n，则A、B两点的水平距离=dn；
    步骤三：AB的坡度==；

    ★请按照下列求解过程完成填空，并把所得结果直接写在答题卡上。
    某中学学生小明和小丁生活在山城，如图3(示意图)，小明每天上学从家A经过B沿着公路AB、BP到学校P，小丁每天上学从家C沿着公路CP到学校P。该山城等高线地形图的比例尺为1：50000，在等高线地形图上量得AB=1.8厘米，BP=3.6厘米，CP=4.2厘米。
    (1) 分别求出AB、BP、CP的坡度(同一段路中间坡度的微小变化忽略不计)；
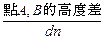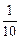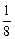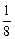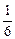    (2) 若他们早晨7点同时步行从家出发，中途不停留，谁先到学校？(假设当坡度在到之间时，小明和小丁步行的平均速度均约为1.3米/秒；当坡度在到之间时，小明和小丁步行的平均速度均约为1米/秒)
    解：(1) AB的水平距离=1.8´50000=90000(厘米)=900(米)，AB的坡度==；
    BP的水平距离=3.6´50000=180000(厘米)=1800(米)，BP的坡度==；
    CP的水平距离=4.2´50000=210000(厘米)=2100(米)，CP的坡度="  " j  ；
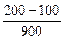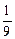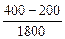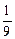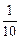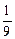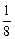    (2) 因为<<，所以小明在路段AB、BP上步行的平均速度均约为1.3米/秒。 因为 k  ，所以小丁在路段CP上步行的平均速度约为  l  米/秒，斜坡 AB的距离=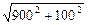»906(米)，斜坡BP的距离=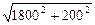»1811(米)，斜 坡CP的距离=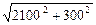»2121(米)，所以小明从家到学校的时间=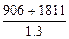=2090(秒)。
    小丁从家到学校的时间约为  m  秒。因此，  n  先到学校。

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    为了扶持农民发展农业生产，国家对购买农机的农户给予农机售价13%的政府补贴．某市农机公司筹集到资金130万元，用于一次性购进A、B两种型号的收割机共30台（购机费用不超过筹集资金）．根据市场需求，这些收割机可以全部销售，全部销售后利润不少于15万元．其中，收割机的进价和售价见下表：
     
    		A型收割机
    		B型收割机
    进价（万元/台）
    		5.3
    		3.6
    售价（万元/台）
    		6
    		4
    设公司计划购进A型收割机x台，收割机全部销售后公司获得的利润为y万元．
    （１）试写出y与x的函数关系式；
    （２）市农机公司有哪几种购进收割机的方案可供选择？
    （３）选择哪种购进收割机的方案，农机公司获利最大？最大利润是多少？此种情况下，购买这30台收割机的所有农户获得的政府补贴总额W为多少万元？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图所示，一只老鼠沿A→B→D的路线逃跑，一只猫同时从阶梯（折线）沿A→C→D的路线去追，结果在距离C点0.6米的D处，猫捉住了老鼠．已知老鼠的速度是猫的
    11
    14
    ，请将下表中每一句话“译成”数学语言（列代数式）．
    设梯级（折线）A→C的长度为xm
    AB+BC的长度为______
    A→C→D的长度为______
    A→B→D的长度为______
    设猫捉住老鼠所用时间为ts
    猫的速度是______
    老鼠的速度是______
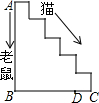
    本题中还有一个条件未用，你能不能利用这个条件将有关的代数式连接起来？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    蜡烛的剩余长度与蜡烛燃烧的时间有关，测得某根蜡烛燃烧的有关数据如下表：
    蜡烛燃烧的时间/min01234…
    蜡烛剩余长度/cm2019.619.218.818.4…
    （1）根据上表，写出蜡烛燃烧nmin后蜡烛剩余长度的表达式；
    （2）根据上式，求蜡烛燃烧14min后的长度．
    （3）照明一天，至少需要几根蜡烛？（一天按24小时计算）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知某市出租车收费标准如y：乘车里程不超过3千米的一律收费11元；乘车里程超过3千米，除了收费11元外，超过部分按每千米2.0元收费．
    （1）乘客甲乘车行驶了9千米（9＞3），请用含9的代数式表示甲应付的车费．
    （2）乘客乙乘车行驶了20千米，他应付她少车费？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，是某广告公司为某商品设计的商标图案，若每个小长方形的长为x，宽为y，求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    依法纳税是公民应有的义务，《个人所得税法》规定，每月总收入减去2000元后的余额为应纳税所得额，应纳税所得额不超过500元的部分按5%纳税；超过500元但不超过2000元的部分按10%纳税，若职工小李某月税前总收入3200元，则该月他应纳税_______元．

    查看答案和解析>>

    同步练习册答案