
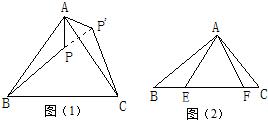
 解:(1)将△ABP绕顶点A旋转到△ACP′处,
解:(1)将△ABP绕顶点A旋转到△ACP′处,


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:阅读理解
| 5 |
| 3 |
| 3 |
| 3 |
| 7 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| 3 |
| 3 |
| 7 |
| 2 |
| 7 |
| 2 |
| 2 |
| 5 |
| 1 | ||
|
1×
| ||||
|
| ||
| 2 |
| 1 | ||||
|
| ||||||||
(
|
| ||||
(
|
| ||||
| 3-2 |
| ||||
| 2 |
| 3 |
| 2 |
| 1 | ||
|
| 2 | ||
|
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
查看答案和解析>>
科目:初中数学 来源:2011—2012学年安徽全椒八年级下第三次月考数学试卷(带解析) 题型:解答题
阅读下面材料,并解决问题:
(1)如下图1,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5则∠APB=______,由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌_______这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
(2)请你利用第(1)题的解答思想方法,解答下面问题:已知:如图2,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2.
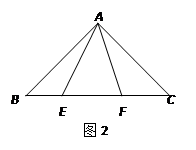
查看答案和解析>>
科目:初中数学 来源:2013届安徽全椒八年级下第三次月考数学试卷(解析版) 题型:解答题
阅读下面材料,并解决问题:
(1)如下图1,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5则∠APB=______,由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌_______这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
(2)请你利用第(1)题的解答思想方法,解答下面问题:已知:如图2,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2.

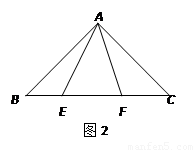
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读下面材料,并解决问题:
(1)如图(10),等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5则
∠APB=__________。
分析:由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌__________这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
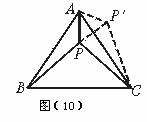
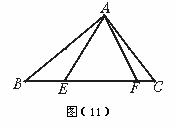
(2)请你利用第(1)题的解答思想方法,解答下面问题:已知如图(11),△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com