
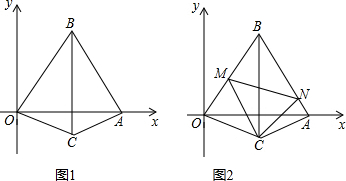
分析 (1)如果△OCD为等腰三角形,那么分点D在OA边或者OB边上或AB边上三种情形.每一种情形,都有可能O为顶点,C为顶点,D为顶点,分别讨论,得出结果;
(2)延长BA至点F,使AF=OM,连接CF,则由SAS可证△MOC≌△FAC,得出MC=CF,再由SAS证出△MCN≌△FCN,得出MN=NF,那么△BMN的周长=BA+BO=4;
(3)过点C作CH⊥OA于点H,根据OC=AC,∠C=120°,求出AC的长度,又∠CAB=∠CAH+∠OAB=90°,所以CA⊥NF,由(2)知△MCN≌△FCN,MN=NF.所以S△MCN=S△FCN,即可解答.
解答 解:(1)如图1,
若点D在OA上时,OC=OD,则OD=OC=$\frac{2\sqrt{3}}{3}$,
D点的坐标为($\frac{2\sqrt{3}}{3}$,0),
如图2,
若OD=CD时,
∵∠COD=30°,cos∠COD=$\frac{DQ}{OD}$,
∴cos30°=$\frac{DQ}{OD}$,
∴OD=$\frac{OQ}{cos3{0}^{°}}=\frac{2}{3}$,
∴D点的坐标为($\frac{2}{3}$,0);
如图3,当点D在BA上时,
若OD=CD,则点D在OC的垂直平分线上,设OC的垂直平分线DQ与x轴交于点P,
则∠APD=60°,OQ=CQ=$\frac{\sqrt{3}}{3}$,
∵∠DAP=60°,
∴△ADP是等边三角形,
过点D作DM⊥PA于M,则PM=DM,
∵∠AOC=30°,
∴OP=$\frac{OQ}{c0s3{0}^{°}}=\frac{2}{3}$,
∴AP=2-$\frac{2}{3}=\frac{4}{3}$,
∴PM=$\frac{2}{3}$,
∴OM=$\frac{4}{3}$,DM=tan60°•PM=$\frac{2\sqrt{3}}{3}$,
∴D点的坐标为($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$);
如图4,当点D在OB上时,
若OD=OC,则OD=$\frac{2\sqrt{3}}{3}$,
过点D作DM⊥OA于M,则OM=$\frac{1}{2}$OD=$\frac{\sqrt{3}}{3}$,DM=1,
则D点的坐标为($\frac{\sqrt{3}}{3}$,1);
故答案为:($\frac{\sqrt{3}}{3}$,1)或($\frac{2\sqrt{3}}{3}$,0)或($\frac{2}{3}$,0)或($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$);
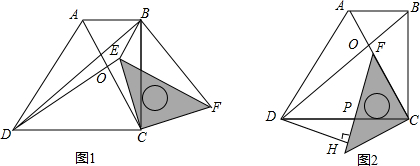
(2)△BMN的周长不发生变化.理由如下:
如图5,延长BA至点F,使AF=OM,连接CF.
又∵∠MOC=∠FAC=90°,OC=AC,
∴△MOC≌△FAC,
∴MC=CF,∠MCO=∠FCA.
∴∠FCN=∠FCA+∠NCA=∠MCO+∠NCA
=∠OCA-∠MCN
=60°,
∴∠FCN=∠MCN.
在△MCN和△FCN中,
$\left\{\begin{array}{l}{MC=CF}\\{∠FCN=∠MCN}\\{CN=CN}\end{array}\right.$,
∴△MCN≌△FCN,
∴MN=NF.
∴BM+MN+BN=BM+NF+BN=BO-OM+BA+AF=BA+BO=4.
∴△BMN的周长不变,其周长为4.
(5)如图6,过点C作CH⊥OA于点H,
∵OA=2,OC=AC,∠OCA=120°,
∴OH=AH=$\frac{1}{2}$OA=1,∠COH=∠CAH=30°,
∴AC=$\frac{AH}{cos3{0}^{°}}=\frac{1}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{3}}{3}$,
∵△ABC为等边三角形,
∴∠OAB=60°,
∴∠CAB=∠CAH+∠OAB=90°,
∴CA⊥NF,
由(2)知△MCN≌△FCN,MN=NF.
∴S△MCN=S△FCN,MN=NF=x,
∵S△FCN=$\frac{1}{2}NF•AC$=$\frac{1}{2}x•\frac{2\sqrt{3}}{3}=\frac{\sqrt{3}}{3}x$,
∴S=$\frac{\sqrt{3}}{3}$x
点评 本题主要考查了等腰三角形、等边三角形的性质,全等三角形的判定,关键是根据题意画出图形,注意分类讨论时,做到不重复,不遗漏.


科目:初中数学 来源: 题型:解答题
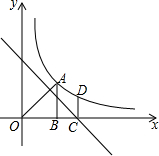 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2,2),过点A作AB⊥x轴,交x轴于点B,在x轴上有一点C,点C在点B的右侧,过点C作直线OA的垂线l,在反比例函数图象上有一点D,点B和点D关于直线l对称.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2,2),过点A作AB⊥x轴,交x轴于点B,在x轴上有一点C,点C在点B的右侧,过点C作直线OA的垂线l,在反比例函数图象上有一点D,点B和点D关于直线l对称.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
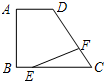 已知:如图,直角梯形ABCD中,AD∥BC,∠A=90°,BC=CD=10,$sinC=\frac{4}{5}$,若点E,F分别是BC,CD上的动点,点E从点B出发向点C运动,点F从点C出发向点D运动,若两点均以每秒1个单位的速度同时出发,连接EF.求△EFC面积的最大值为10.
已知:如图,直角梯形ABCD中,AD∥BC,∠A=90°,BC=CD=10,$sinC=\frac{4}{5}$,若点E,F分别是BC,CD上的动点,点E从点B出发向点C运动,点F从点C出发向点D运动,若两点均以每秒1个单位的速度同时出发,连接EF.求△EFC面积的最大值为10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
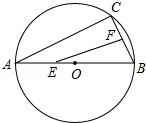 如图,AB是⊙O的直径,弦AC=8cm,BC=6cm,若动点E以2cm/s的速度从A向B运动,点F以1cm/s的速度从B向C运动,设运动时间为t(s),连接EF,当△BEF是直角三角形时,求t(s)的值.
如图,AB是⊙O的直径,弦AC=8cm,BC=6cm,若动点E以2cm/s的速度从A向B运动,点F以1cm/s的速度从B向C运动,设运动时间为t(s),连接EF,当△BEF是直角三角形时,求t(s)的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
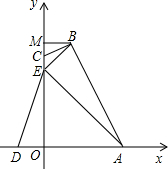 如图,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,过点B作BM⊥y于点M,OE=OA=3,OD=1,连接AE、BE、DE.已知tan∠CBE=$\frac{1}{3}$,B(1,4).
如图,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,过点B作BM⊥y于点M,OE=OA=3,OD=1,连接AE、BE、DE.已知tan∠CBE=$\frac{1}{3}$,B(1,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com