
【题目】如图1所示在矩形ABCD中,AB=6,AD=3,点E、F分别是边DC、DA的三等分点(DE![]() EC,DF
EC,DF![]() AF),四边形DFGE为矩形,连接BG.
AF),四边形DFGE为矩形,连接BG.
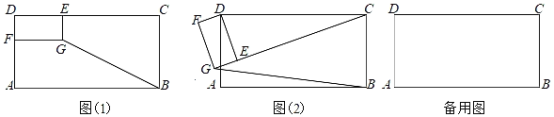
(1)问题发现:在图(1)中,![]() = ;
= ;
(2)拓展探究:将图(1)中的矩形DFGE绕点D旋转一周,在旋转过程中![]() 的大小有无变化?请仅就图(2)的情形给出证明;
的大小有无变化?请仅就图(2)的情形给出证明;
(3)问题解决:当矩形DFGE旋转至B、G、E三点共线时,请直接写出线段CE的长.
【答案】(1)![]() ;(2)不变,证明见解析;(3)
;(2)不变,证明见解析;(3)![]()
【解析】
(1)如图1中,延长FG交BC于H.在解直角三角形求出EC,BG即可解决问题.
(2)结论:![]() 的大小不变.
的大小不变.![]() .如图2中,连接BD,DG.证明△CDE∽△BDG,可得
.如图2中,连接BD,DG.证明△CDE∽△BDG,可得 .
.
(3)分两种情形:①如图3﹣1中,当点G落在BG上时,利用勾股定理以及(2)中结论即可解决问题.②如图3﹣2中,当点G落在BE上时,同法可得EC的长.
解:(1)如图1中,延长FG交BC于H.
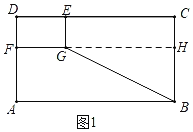
∵四边形ABCD,四边形DEGF都是矩形,
∴DE=FG=![]() AB=2,DF=EG=
AB=2,DF=EG=![]() AD=1,∠C=∠CEG=∠EGH=90°,
AD=1,∠C=∠CEG=∠EGH=90°,
∴四边形ECHG是矩形,
∴EC=GH=4,EG=CH=1,BH=BC﹣CH=3﹣1=2,
∴BG=![]() ,
,
∴![]() ,
,
故答案为![]() .
.
(2)结论:![]() 的大小不变,
的大小不变,![]() .
.
理由:如图2中,连接BD,DG.

∵![]() ,
,
∴![]() ,
,
∵∠DCB=∠DEG=90°,
∴∠CDB=∠EDG,![]() ,
,
∴∠CDE=∠BDG,![]() ,
,
∴△CDE∽△BDG,
∴ .
.
(3)①如图3﹣1中,当点G落在BG上时,
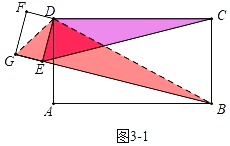
在Rt△DEB中,∵DE=2.BD=3![]() ,
,
∴BE=![]() ,
,
∴BG=EG+BE=1+![]() ,
,
∴CE=![]() BG=
BG=![]() +
+![]() .
.
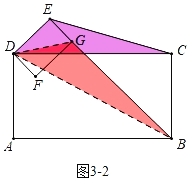
②如图3﹣2中,当点G落在BE上时,同法可得EC=![]() ﹣
﹣![]() .
.
综上所述,满足条件的EC的值为![]() ±
±![]() .
.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】定义:对于函数y,我们称函数|y|叫做函数y的正值函数.例如:函数y=![]() 的正值函数为y=|
的正值函数为y=|![]() |.如图为曲线y=
|.如图为曲线y=![]() (x>0).
(x>0).
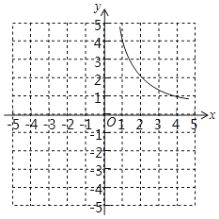
(1)请你在图中画出y=x+3的正值函数的图象并写出y=x+3的正值函数的两条性质;
(2)设y=x+3的正值函数的图象与x轴、y轴、曲线y=![]() (x>0)的交点分别是A,B,C.点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与正值函数图象交于另一点E,与曲线交于点P.试求△PAD的面积的最大值;
(x>0)的交点分别是A,B,C.点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与正值函数图象交于另一点E,与曲线交于点P.试求△PAD的面积的最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
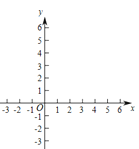
(1)求抛物线的表达式;
(2)直线![]() 平行于
平行于![]() 轴,与抛物线交于
轴,与抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,求线段
,求线段![]() 的长;
的长;
(3)点![]() 是该抛物线上一点,且在第一象限内,联结
是该抛物线上一点,且在第一象限内,联结![]() 、
、![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,![]() 点朝上是必然事件
点朝上是必然事件
B.了解一批灯泡的使用寿命,适合用普查的方式.
C.从五张分别写着![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的卡片中随机抽取
的卡片中随机抽取![]() 张,是无理数的概率是
张,是无理数的概率是![]() .
.
D.甲乙两人在相同条件下各射击![]() 次,他们的成绩平均数相同,方差分别是
次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定.
,则甲的射击成绩较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A、B、C、D四种不同口味的牛奶供学生饮用,学校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如图所示的两幅不完整的统计图,根据统计图的信息解决下列问题:
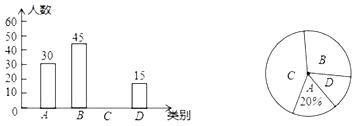
(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的圆心角度数是 ;
(4)若该校有400名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A、B口味的牛奶共约多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,OC长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD =![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
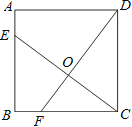
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
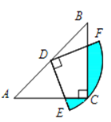
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=![]() ,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为_______.
,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com