
����Ŀ��ij��Ҫ����һ��Բ����ˮ�أ���ˮ�����봹ֱ��ˮ�氲װһ������![]() ����
����![]() ǡ����ˮ�����ģ���װ�����Ӷ���
ǡ����ˮ�����ģ���װ�����Ӷ���![]() ����Բ����ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�
����Բ����ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�![]() ������ƽ���ϣ�ˮ������ĸ߶�
������ƽ���ϣ�ˮ������ĸ߶�![]() ��ˮƽ����
��ˮƽ����![]() ֮��Ĺ�ϵ��ͼ��ʾ������ƽ��ֱ������ϵ���ұ������ߵĹ�ϵʽΪ
֮��Ĺ�ϵ��ͼ��ʾ������ƽ��ֱ������ϵ���ұ������ߵĹ�ϵʽΪ![]() .������������⣺
.������������⣺

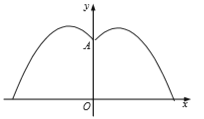
��1����![]() ��Ϊ
��Ϊ![]() ����ʽ����д�������ˮ����ˮƽ������߶��Ƕ����ף�
����ʽ����д�������ˮ����ˮƽ������߶��Ƕ����ף�
��2��д��������������ߵı���ʽ��
��3�������������أ���Ҫʹ�����ˮ�����ڳ��ڣ�ˮ�ص�ֱ������Ҫ�����ף�
���𰸡���1�������ˮ����ˮƽ������߶���4��.��2��![]() .��3��ˮ�ص�ֱ������Ҫ6��.
.��3��ˮ�ص�ֱ������Ҫ6��.
��������
��1�������䷽����һ��ʽת��Ϊ����ʽ��������������ˮ����ˮƽ������߶ȣ�
��2�������������ߵĹ���y��Գƣ����������������ߵĶ�����ϵ���Ͷ������꣬�Ӷ������������ߵĽ���ʽ��
��3��������ұ���������x��Ľ���ĺ����꣬���öԳ��Լ������ˮ�ص�ֱ������Сֵ.
�⣺��1����![]() ��
��
�������ߵĶ���ʽΪ![]() .
.
�������ˮ����ˮƽ������߶���4��.
��2�����������ߵĹ���y��Գ�
����������ߵ�a=-1����������Ϊ��-1,4��
��������ߵı���ʽΪ![]() .
.
��3����![]() ����
����![]() ����
����
��![]() ��
��
���![]() ��
��![]() ������������x����ҽ��㣬�ʲ������⣬��ȥ��.
������������x����ҽ��㣬�ʲ������⣬��ȥ��.
��![]() ���ף�
���ף�
��ˮ�ص�ֱ������Ҫ6��.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
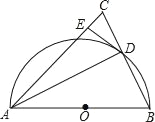
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����ABΪֱ������Բ��O����BC�ڵ�D������AD������D��DE��AC������Ϊ��E��
��1����֤��DE����O�����ߣ�
��2������O�뾶Ϊ3��CE��2ʱ����BD����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC����ACΪֱ���ġ�O��AB�ڵ�D����EΪ��AD���е㣬����CE��AB�ڵ�F����BF=BC��

��1����֤��BC�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ2��![]() =
=![]() ����CE�ij���
����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪������![]() ���䶥��ΪA��
���䶥��ΪA��
��1��д�����������ߵĿ��ڷ�����A�����꣬��˵�����ı仯�����
��2��ֱ��BCƽ����x�ᣬ��������������B��C���㣨��B�ڵ�C��ࣩ����![]() �����B���꣮
�����B���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
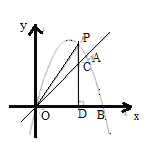
����Ŀ����ͼ����֪������![]() ��ͼ����
��ͼ����![]() ��
��![]() ��ԭ��
��ԭ��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() �Ϸ��������ϵ�һ�����㣮
�Ϸ��������ϵ�һ�����㣮
��1����ֱ��![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
��2������![]() ��
��![]() ��Ĵ��ߣ�����Ϊ
��Ĵ��ߣ�����Ϊ![]() ������ֱ��
������ֱ��![]() ���ڵ�
���ڵ�![]() ����
����![]() Ϊ����������ʱ����
Ϊ����������ʱ����![]() �����ꣻ
�����ꣻ
��3����![]() ���ڶԳ���ĵ�Ϊ
���ڶԳ���ĵ�Ϊ![]() �������ߵĶ���Ϊ
�������ߵĶ���Ϊ![]() ��̽���Ƿ����һ��
��̽���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() �����Ϊ
�����Ϊ![]() ��������ڣ����
��������ڣ����![]() �����ꣻ��������ڣ���˵�����ɣ�
�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ţ���������ˮ��2mʱ��ˮ���4m��ˮ���½�2m��ˮ���������______m.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������״����С���ʵ���ȫһ����3�������2����������˵����ȷ���ǣ�������
A.����������һ����һ���Ǻ���
B.�Ӵ��г��һ������ٴӴ��г��һ�����ֺ�������ĸ���һ����
C.�Ӵ���������2�����ֶ��Ǻ���ĸ���Ϊ![]()
D.�Ӵ��г��2��������ɫ��ͬ����ĸ�����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC��90����D��BC���е㣬E��AD���е㣬����A��AF��BC��BE���ӳ����ڵ�F��

��1����֤���ı���ADCF�����Σ�
��3����AC��6��AB��8��������ADCF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1���ⷽ�̣��٣�2x��3��2��25
��![]() ��
��![]() ��x
��x
��2���Ȼ�������ֵ����1��![]() ����
����![]() ��
��![]() ������x����x2��x��l��0
������x����x2��x��l��0
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com