
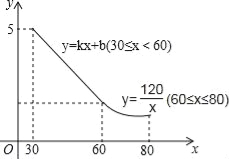
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?
【答案】(1)y=﹣0.1x+8(30≤x≤60)(2)w=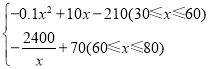 (3)当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元
(3)当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元
【解析】
试题分析:(1)由图象知,当30≤x≤60时,图象过(60,2)和(30,5),运用待定系数法求解析式即可;
(2)根据销售产品的纯利润=销售量×单个利润,分30≤x≤60和60<x≤80列函数表达式;
(3)当30≤x≤60时,运用二次函数性质解决,当60<x≤80时,运用反比例函数性质解答.
试题解析:(1)当x=60时,y=![]() =2,
=2,
∴当30≤x≤60时,图象过(60,2)和(30,5),
设y=kx+b,则
![]() ,
,
解得:![]() ,
,
∴y=﹣0.1x+8(30≤x≤60);
(2)根据题意,当30≤x≤60时,W=(x﹣20)y﹣50=(x﹣20)(﹣0.1x+8)﹣50=﹣0.1x2+10x﹣210,
当60<x≤80时,W=(x﹣20)y﹣50=(x﹣20)·![]() ﹣50=﹣
﹣50=﹣![]() +70,
+70,
综上所述:W=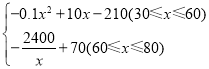 ;
;
(3)当30≤x≤60时,W=﹣0.1x2+10x﹣210=﹣0.1(x﹣50)2+40,
当x=50时,W最大=40(万元);
当60<x≤80时,W=﹣![]() +70,
+70,
∵﹣2400<0,W随x的增大而增大,
∴当x=80时,W最大=﹣![]() +70=40(万元),
+70=40(万元),
答:当销售价格定为50元/件或80元/件,获得利润最大,最大利润是40万元.


科目:初中数学 来源: 题型:
【题目】问题原型:如图①,在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,在AD上取点E,使DE=CD,连结BE.求证:BE=AC.
问题拓展:如图②,在问题原型的条件下,F为BC的中点,连结EF并延长至点M,使FM=EF,连结CM.
(1)判断线段AC与CM的大小关系,并说明理由.
(2)若AC=![]() ,直接写出A、M两点之间的距离.
,直接写出A、M两点之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
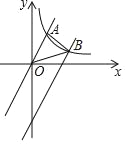
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,m);将直线y=
(x>0)的图象交于点A(2,m);将直线y=![]() x向下平移后与反比例函数y=
x向下平移后与反比例函数y=![]() (x>0)的图象交于点B,且△AOB的面积为3.
(x>0)的图象交于点B,且△AOB的面积为3.
(1)求k的值;
(2)求平移后所得直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
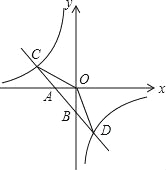
【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数![]() 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数y1=k1x+b与反比例函数![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
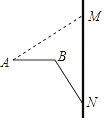
【题目】高铁给我们的出行带来了极大的方便.如图,“和谐号”高铁列车座椅后面的小桌板收起时,小桌板的支架的底端N与桌面顶端M的距离MN=75cm,且可以看作与地面垂直.展开小桌板使桌面保持水平,AB⊥MN,∠MAB=∠MNB=37°,且支架长BN与桌面宽AB的长度之和等于MN的长度.求小桌板桌面的宽度AB(结果精确到1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
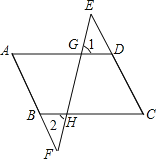
【题目】完成下面的说理过程:如图,在四边形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 延长线上的点,连接
延长线上的点,连接![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .已知
.已知![]() ,
,![]() .对
.对![]() 和
和![]() 说明理由.
说明理由.
理由:![]() (已知),
(已知),
![]() (______),
(______),
![]() (等量代换).
(等量代换).
![]() (______).
(______).
![]() (______).
(______).
![]() (______),
(______),
![]() (______).
(______).
![]() (______).
(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的大学生自愿者参与服务工作,计划组织全校自愿者统一乘车去某地.若单独调配![]() 座客车若干辆,则空出
座客车若干辆,则空出![]() 个座位,若只调配
个座位,若只调配![]() 座客车若干辆,则用车数量将增加
座客车若干辆,则用车数量将增加![]() 辆,并有
辆,并有![]() 人没有座位.
人没有座位.
(1)计划调配![]() 座客车多少辆?该大学共有多少名自愿者?(列方程组解答)
座客车多少辆?该大学共有多少名自愿者?(列方程组解答)
(2)若同时调配![]() 座和
座和![]() 座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
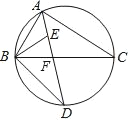
【题目】如图,∠BAC的平分线交AABC的外接圆于点D,交BC于点F,∠ABC的平分线交AD于点E.
(1)求证:DE=DB.
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径;
(3)若BD=6,DF=4,求AD的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com