
【题目】已知抛物线![]() 的顶点为
的顶点为![]() ,其部分图象如图所示,给出下列四个结论:①
,其部分图象如图所示,给出下列四个结论:①![]() ; ②
; ②![]() ;③
;③![]() ;④若点
;④若点![]() 在抛物线上,则
在抛物线上,则![]() .其中结论正确的是( )
.其中结论正确的是( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】由抛物线开口向下,可知a<0; 故①正确.
抛物线与x轴有两个交点,故b 4ac>0,故②正确.
由抛物线的顶点![]() 可知对称轴为直线x=-1,可知
可知对称轴为直线x=-1,可知![]() =-1,从而有
=-1,从而有![]() ; 故③正确.
; 故③正确.
![]() 为x=
为x=![]() 时的函数值,
时的函数值, ![]() 为x=-1时的函数值,根据函数图象可知
为x=-1时的函数值,根据函数图象可知![]() ,故④正确.
,故④正确.
综上可知应选D.
点睛: 本题主要考查二次函数图象的性质,二次函数图象的三要素为开口方向、对称轴、顶点. 1、当a>0时,开口向上;当a<0时,开口向下.
2、b和a共同决定二次函数对称轴的位置,二次函数y=a×x2+bx+c(a≠0)的对称轴是直线x=![]() .
.
ba>0(即a、b同号)时,对称轴在y轴左侧;ba<0(即a、b异号)时,对称轴在y轴右侧.
c的大小决定二次函数y=a×x2+bx+c(a≠0)与y轴交点的位置,当x=0时,y=c.
3、b4ac的值决定抛物线与x轴的交点个数.b4ac>0<=>抛物线与x轴有两个交点;b4ac=0<=>抛物线与x轴有一个公共点;b4ac<0<=>抛物线与x轴没有交点.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程组
的方程组![]() ,
,
(1)若用代入法求解,可由①得:![]() = ③,把③代入②解得
= ③,把③代入②解得![]() = ,将其代入③解得
= ,将其代入③解得![]() = ,∴原方程组的解为 ;
= ,∴原方程组的解为 ;
(2)若此方程组的解![]() 互为相反数,求这个方程组的解及
互为相反数,求这个方程组的解及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
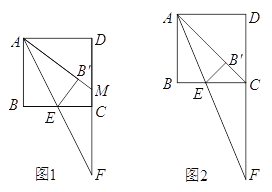
【题目】如图,正方形ABCD的边长为12,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B'处.
(1)当![]() =1时,如图1,延长A B',交CD于点M,①CF的长为 ;②求证:AM=FM.
=1时,如图1,延长A B',交CD于点M,①CF的长为 ;②求证:AM=FM.
(2)当点B'恰好落在对角线AC上时,如图2,此时CF的长为 ; ![]() = .
= .
(3)当![]() =3时,求∠DA B'的正弦值.
=3时,求∠DA B'的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程x(x+1)=x+1的解是( )
A. x1=0,x2=-1 B. x = 1 C. x1 = x2 = 1 D. x1 = 1,x2=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物![]() 元(
元(![]() ).
).
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
, ![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 边上的动点(不含端点),且
边上的动点(不含端点),且![]() 、
、![]() 均过正方形的中心
均过正方形的中心![]() .
.
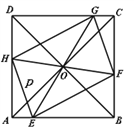
(1)填空: ![]()
![]() (“>”、“<”、“=”);
(“>”、“<”、“=”);
(2)当四边形![]() 为矩形时,请问线段
为矩形时,请问线段![]() 与
与![]() 应满足什么数量关系;
应满足什么数量关系;
(3)当四边形![]() 为正方形时,
为正方形时, ![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com