
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据等腰三角形的性质,等式的性质,全等三角形的性质以及直角三角形的性质对各小题分析判断即可得解.
解答 解:①等腰三角形两腰上的高相等,正确;逆命题:两边上的高相等的三角形是等腰三角形,正确,所以原命题与逆命题都是真命题;
②若a>b,则ac2>bc2,错误,c=0不成立;逆命题:若ac2>bc2,a>b,正确,是真命题;
③全等三角形对应角相等,正确;逆命题:对应角相等的三角形是全等三角形,错误,可以是相似三角线;
④直角三角形两锐角互余,正确;逆命题:两锐角互余的三角形是直角三角形,正确,所以原命题与逆命题都是真命题.
综上所述,原命题与逆命题都是真命题是①④共2个.
故选B.
点评 本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.


科目:初中数学 来源: 题型:解答题
 如图,将矩形纸片AFCD沿对角线AC折叠得到如图所示的图形,AB与CD交于点E.
如图,将矩形纸片AFCD沿对角线AC折叠得到如图所示的图形,AB与CD交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
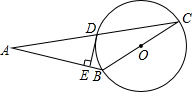 如图,在△ABC中,AB=BC,以BC为直径的⊙O与AC交于点D,DE⊥AB于点E.
如图,在△ABC中,AB=BC,以BC为直径的⊙O与AC交于点D,DE⊥AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com