练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，BC=2，∠A=70°，以BC边为直径作⊙O，分别交AB，AC于点D，E，连接DO，EO，则S扇形OBD+S扇形OEC= ． （结果用π表示）

    【答案】 π
    【解析】解：连接BE，
    ∵BC是直径，
    ∴AC⊥BE，
    ∴∠ABE=90°﹣∠A=20°，
    ∴∠DOE=2∠ABE=40°，
    ∴∠DOB+∠COE=140°，
    又∵两个扇形的半径都是1，
    ∴S扇形OBD+S扇形OEC= = π．
    所以答案是： π．

    【考点精析】通过灵活运用圆周角定理和扇形面积计算公式，掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=x2+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（﹣1，0）．

    （1）求抛物线的解析式及顶点D的坐标；

    （2）判断△ABC的形状，证明你的结论；

    （3）点M是x轴上的一个动点，当△DCM的周长最小时，求点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读解题过程,回答问题.

    如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.

    解:过O点作射线OM,使点M,O,A在同一直线上.

    因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,所以∠BOC=∠MOD,

    所以∠AOD=180°-∠BOC=180°-30°=150°.

    (1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?

    (2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将边长为2cm的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，若两个三角形重叠部分的面积为1cm2，则它移动的距离AA′等于（ ）

    A. 0.5cm B. 1cm C. 1.5cm D. 2cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】规定※是一种新的运算符号，且a※b=ab+a+b，例如：2※3=2×3+2+3=11，那么（3※4）※1=（ ）
    A.19
    B.29
    C.39
    D.49

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】方程﹣2x﹣1＝1的解为x＝_____

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为∣AB∣.

    当A、B两点中有一点在原点时，不妨设点A在原点，

    如图1，∣AB∣＝∣OB∣＝∣b∣＝∣a-b∣；

    当A、B两点都不在原点时，

    如图2，点A、B都在原点的右边

    ∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣；

    如图3，点A、B都在原点的左边，

    ∣AB∣＝∣OB∣－∣OA∣＝∣b∣-∣a∣=－b-（-a）=∣a-b∣；

    如图4，点A、B在原点的两边，

    ∣AB∣＝∣OB∣+∣OA∣＝∣a∣+∣b∣= a +（-b）=∣a-b∣；

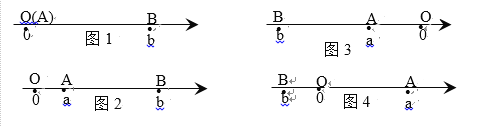
    回答下列问题：

    （1）数轴上表示3和7的两点之间的距离是 ,数轴上表示－1和－3的两点之间的距离是 ,数轴上表示1和－2的两点之间的距离是 .

    （2）数轴上表示x和－2的两点A和B之间的距离是 ,如果∣AB∣＝2，那么x为 ；

    （3）当代数式∣x∣+∣x-1∣取最小值时，最小值是 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中，假命题是（ ）

    A.一组对边相等，另一组对边平行的四边形是平行四边形 B.三个角是直角的四边形是矩形

    C.四边相等的四边形是菱形D.有一个角是直角的菱形是正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为判断命题“有三条边相等且一组对角相等的四边形是菱形”的真假，数学课上，老师给出菱形ABCD如图1，并作出了一个四边形ABC′D．具体作图过程如下：
    如图2，在菱形ABCD中，
    ①连接BD，以点B为圆心，以BD的长为半径作圆弧，交CD于点P；
    ②分别以B、D为圆心，以BC、PC的长为半径作圆弧，两弧交于点C′．
    ③连接BC′、DC′，得四边形ABC′D．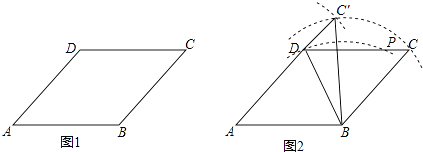

    依据上述作图过程，解决以下问题：
    （1）求证：∠A=∠C′；AD=BC′．
    （2）根据作图过程和（1）中的结论，说明命题“有三条边相等且有一组对顶角相等的四边形是菱形”是命题．（填写“真”或“假”）

    查看答案和解析>>

    同步练习册答案