
 坐标系,根据题中提供的信息,求绳子所在抛物线的函数关系式;
坐标系,根据题中提供的信息,求绳子所在抛物线的函数关系式;
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
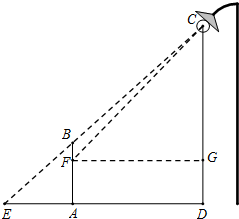 盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB).
盏路灯(可以看成点C),已知点C与点A的铅垂距离CD=9m,水平距离AD=6.4m(图中CD⊥AD,AD⊥AB).查看答案和解析>>
科目:初中数学 来源: 题型:
| 15 |
| 2 |
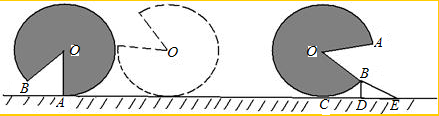
| A、3πcm | ||
| B、4πcm | ||
C、
| ||
| D、5πcm |
查看答案和解析>>
科目:初中数学 来源:江苏省南京三中2011届九年级上学期期末考试数学试题 题型:044
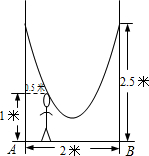
如图,水平地面的A、B两点处有两棵笔直的大树相距2米,小明的父亲在这两棵树间拴了一根绳子,给他做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子.

(1)请完成如下操作:以AB所在直线为x轴、线段AB的垂直平分线为y轴,建立平面直角坐标系,根据题中提供的信息,求绳子所在抛物线的函数关系式;
(2)求绳子的最低点离地面的距离.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年江苏省南京市三中九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com