
【题目】一辆货车从百货大楼出发负责送货,向东走了2千米到达小明家,继续向东走了4千米到达小红家,然后向西走了9千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置;
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.5升,那么这辆货车共耗油多少升?
【答案】(1)见解析;(2)5千米;(3)9升.
【解析】
(1)根据已知,以百货大楼为原点,以向东为正方向,用1个单位长度表示1千米一辆货车从百货大楼出发,向东走了2千米,到达小明家,继续向东走了4千米到达小红家,然后西走了9千米,到达小刚家,最后返回百货大楼,则小明家、小红家和小刚家在数轴上的位置可知.
(2)用小明家的坐标减去与小刚家的坐标即可.
(3)这辆货车一共行走的路程,实际上就是2+4+9+3=18(千米),货车从出发到结束行程共耗油量=货车行驶每千米耗油量×货车行驶所走的总路程.
解:(1)如图所示:
![]()
(2)由小明与小刚在数轴上的位置可得:![]() 千米
千米
(3)这辆货车此次送货共耗油:![]() 升
升


科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点P在边AB上,∠CPB的平分线交边BC于点D,DE⊥CP于点E,DF⊥AB于点F.当△PED与△BFD的面积相等时,BP的值为( )
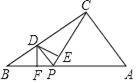
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,试说明DA=DE.
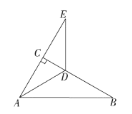
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
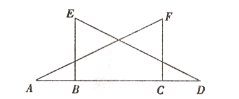
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1B2、△A2B2B3、△A3B3B4、…均为等边三角形,若OB1=1,则△A8B8B9的边长为_____
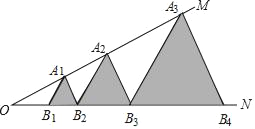
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )
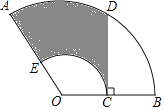
A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,直线![]() 相交于点
相交于点![]() .
.
(1)若∠AOC=35°,求![]() 的度数;
的度数;
(2)若∠BOD:∠BOC=2:4,求![]() 的度数;
的度数;
(3)在(2)的条件下,过点![]() 作
作![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.
(1)求证:FG是⊙O的切线;
(2)若tanC=2,求![]() 的值.
的值.
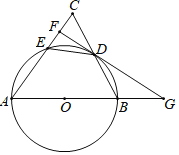
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com