
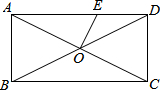
 如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,BC=8,过点O作OE⊥AC交AD于点E,则AE的长为5.
如图,矩形ABCD的对角线AC、BD相交于点O,AB=4,BC=8,过点O作OE⊥AC交AD于点E,则AE的长为5. 分析 连接CE,根据矩形的对边相等可得AD=BC=8,CD=AB=4,根据矩形的对角线互相平分可得OA=OC,然后判断出OE垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AE=CE,设AE=CE=x,表示出DE,然后在Rt△CDE中,利用勾股定理列出方程求解即可.
解答 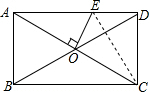 解:如图,∵矩形ABCD中,AB=4,BC=8,
解:如图,∵矩形ABCD中,AB=4,BC=8,
∴AD=BC=8,AB=CD=4,OA=OC,
∵OE⊥AC,
∴OE垂直平分AC,
∴AE=CE,
设AE=CE=x,则DE=8-x,
在Rt△CDE中,CD2+DE2=CE2,
即42+(8-x)2=x2,
解得x=5,
即AE的长为5.
故答案为:5.
点评 本题考查了矩形的性质,线段垂直平分线上的点到两端点的距离相等的性质,勾股定理,熟记各性质并利用勾股定理列出方程是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
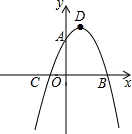 如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.
如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 应试者 | 计算机技能 | 语言表达 | 商品知识 |
| 甲 | 70 | 50 | 80 |
| 乙 | 90 | 75 | 45 |
| 丙 | 50 | 60 | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | |
| 成本(元) | 50 | 35 |
| 利润(元) | 20 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
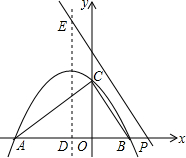 如图,二次函数y=ax2+bx+3的图象抛物线与其对称轴交于点(-1,m),与x轴交于点A和点B(2,0),与y轴交于点C,其对称轴与x轴交于点D.
如图,二次函数y=ax2+bx+3的图象抛物线与其对称轴交于点(-1,m),与x轴交于点A和点B(2,0),与y轴交于点C,其对称轴与x轴交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
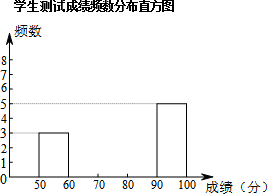 某校九年级有200名学生参加《中小学生国家体质健康标准》测试赛活动.为了解本次测试的成绩分布情况,从中抽取了20名学生的成绩进行分组整理.现已完成前15个数据的整理,还有后5个数据尚未累计:
某校九年级有200名学生参加《中小学生国家体质健康标准》测试赛活动.为了解本次测试的成绩分布情况,从中抽取了20名学生的成绩进行分组整理.现已完成前15个数据的整理,还有后5个数据尚未累计:| 成绩x(分) | 频数累计 | 频数 | 频率 |
| 50≤x<60 | 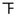 | 3 | 0.15 |
| 60≤x<70 | ▁ | 2 | 0.10 |
| 70≤x<80 | 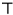 | 4 | 0.20 |
| 80≤x<90 | 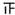 | 6 | 0.30 |
| 90≤x≤100 | 正 | 5 | 0.25 |
| 合计 | 20 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
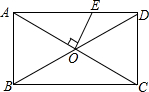 如图所示,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
如图所示,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 1.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com