
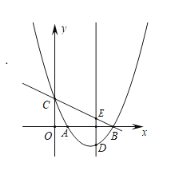
【题目】在平面直角坐标系中,已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0).B(4,0),C(0,2)三点,直线y=kx+t经过B.C两点,点D是抛物线上一个动点,过点D作y轴的平行线,与直线BC相交于点E.
(1)求直线和抛物线的解析式;
(2)当点D在直线BC下方的抛物线上运动,使线段DE的长度最大时,求点D的坐标;
(3)点D在运动过程中,若使O.C.D.E为顶点的四边形为平行四边形时,请直接写出满足条件的所有点D的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+2;(2)D(2,﹣1);(3)点D的坐标是(2,﹣1)或(2+2
x+2;(2)D(2,﹣1);(3)点D的坐标是(2,﹣1)或(2+2![]() ,3﹣
,3﹣![]() )或(2﹣2
)或(2﹣2![]() ,3+
,3+![]() )时,都可以使O.C.D.E为顶点的四边形为平行四边形.
)时,都可以使O.C.D.E为顶点的四边形为平行四边形.
【解析】
(1)利用待定系数法求解可得;
(2)设点D坐标为(m,![]() m2-
m2-![]() m+2),则E点的坐标为(m,-
m+2),则E点的坐标为(m,-![]() m+2),由DE=(-
m+2),由DE=(-![]() m+2)-(
m+2)-(![]() m2-
m2-![]() m+2)=-
m+2)=-![]() m2+2m=-
m2+2m=-![]() (m-2)2+2可得答案;
(m-2)2+2可得答案;
(3)分点D在DE上方和下方两种情况,用m的代数式表示出DE的长度,依据DE=2得出关于m的方程,解之可得.
(1)把点B(4,0),C(0,2)代入直线y=kx+t,
得:![]() ,解得
,解得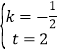 ,
,
∴y=﹣![]() x+2;
x+2;
把点A(1,0).B(4,0),C(0,2)代入y=ax2+bx+c,
得: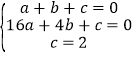 ,解得
,解得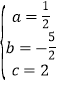 ,
,
∴y=![]() x2﹣
x2﹣![]() x+2;
x+2;
(2)设点D坐标为(m,![]() m2﹣
m2﹣![]() m+2),E点的坐标为(m,﹣
m+2),E点的坐标为(m,﹣![]() m+2),
m+2),
∴DE=(﹣![]() m+2)﹣(
m+2)﹣(![]() m2﹣
m2﹣![]() m+2)=﹣
m+2)=﹣![]() m2+2m=﹣
m2+2m=﹣![]() (m﹣2)2+2,
(m﹣2)2+2,
∴当m=2时,DE的长最大,为2,
当m=2时,![]() m2﹣
m2﹣![]() m+2=﹣1,
m+2=﹣1,
∴D(2,﹣1);
(3)①当D在E下方时,如(2)中,DE=﹣![]() m2+2m,OC=2,OC∥DE,
m2+2m,OC=2,OC∥DE,
∴当DE=OC时,四边形OCED为平行四边形,
则﹣![]() m2+2m=2,解得m=2,此时D(2,﹣1);
m2+2m=2,解得m=2,此时D(2,﹣1);
②当D在E上方时,DE=(![]() m2﹣
m2﹣![]() m+2)﹣(﹣
m+2)﹣(﹣![]() m+2)=
m+2)=![]() m2﹣2m,
m2﹣2m,
令![]() m2﹣2m=2,解得m=2
m2﹣2m=2,解得m=2![]() ,
,
∴此时D(2+2![]() ,3﹣
,3﹣![]() )或(2﹣2
)或(2﹣2![]() ,3+
,3+![]() ),
),
综上所述,点D的坐标是(2,﹣1)或(2+2![]() ,3﹣
,3﹣![]() )或(2﹣2
)或(2﹣2![]() ,3+
,3+![]() )时,都可以使O.C.D.E为顶点的四边形为平行四边形.
)时,都可以使O.C.D.E为顶点的四边形为平行四边形.


科目:初中数学 来源: 题型:
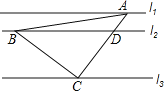
【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2与点D.已知l1与l2的距离为1,l2与l3的距离为3,则线段CD的长等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
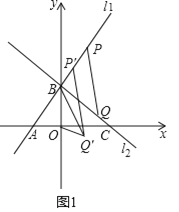
【题目】如图,直线l1:y=![]() x+12与x轴、y轴分别交于A、B两点,直线l2与x轴、y轴分别交于C、B两点,且AB:BC=3:4.
x+12与x轴、y轴分别交于A、B两点,直线l2与x轴、y轴分别交于C、B两点,且AB:BC=3:4.
(1)求直线l2的解析式,并直接判断△ABC的形状(不需说明理由);
(2)如图1,P为直线l1上一点,横坐标为12,Q为直线l2上一动点,当PQ+![]() CQ最小时,将线段PQ沿射线PA方向平移,平移后P、Q的对应点分别为P'、Q',当OQ'+BQ'最小时,求点Q'的坐标;
CQ最小时,将线段PQ沿射线PA方向平移,平移后P、Q的对应点分别为P'、Q',当OQ'+BQ'最小时,求点Q'的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极绘就我市“一福地、四名城”建设的宏伟蓝图,某镇大力发展旅游业,一店铺专门售卖地方特产“曲山老鹅”,以往销售数据表明,该“曲山老鹅”每天销售数量y(只)与销售单价x(元)满足一次函数y=-![]() x+110,每只“曲山老鹅”各项成本合计为20元/只.
x+110,每只“曲山老鹅”各项成本合计为20元/只.
(1)该店铺“曲山老鹅”销售单价x定为多少时,每天获利最大?最大利润是多少?
(2)该店店主关心教育,决定今后的一段时间从每天的销售利润中捐出200元给当地学校作为本学期优秀学生的奖励资金,为了保证该店捐款后每天剩余利润不低于4000元,试确定该“曲山老鹅”销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如下不完整统计图.
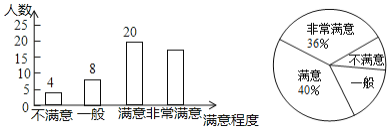
请结合图中信息,解决下列问题:
(1)此次调查中接受调查的人数为多少人,其中“非常满意”的人数为多少人;
(2)兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访,已知这4位群众中有2位来自甲片区,另2位来自乙片区,请用画树状图或列表的方法求出选择的群众来自甲片区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
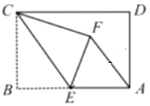
【题目】矩形ABCD中,AB=4,BC=3,点E为AB的中点,将矩形ABCD沿CE折叠,使得点B落到点F的位置.
(1)求证:AF∥CE.
(2)求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝即将到来的“三月三”壮族传统节日,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成如下图表:
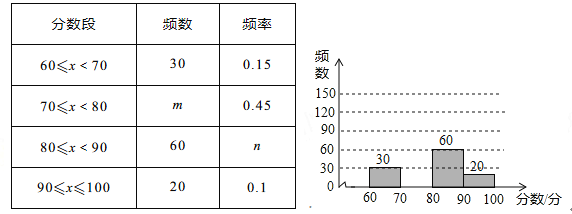
请根据如上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生,表中的数![]() .
.![]() .
.
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段![]() 所对应扇形的圆心角为 度;
所对应扇形的圆心角为 度;
(4)全校共有![]() 名学生参加比赛,估计该校成绩
名学生参加比赛,估计该校成绩![]() 范围内的学生有多少人?
范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com