练习册

  • 练习册
  • 试题
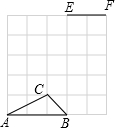    精英家教网 > 初中数学 > 题目详情

    在小正方形的网格中，下列四个选项中的三角形，与如图所示的三角形相似的是


    1. A.
    2. B.
    3. C.
    4. D.
    B
    分析：根据网格结构以及勾股定理可得所给图形是两直角边分别为、2的直角三角形，然后利用相似三角形的判定方法选择答案即可．
    解答：根据勾股定理，所给图形的两直角边为=，
    =2，
    所以，夹直角的两边的比为=，
    纵观各选项，只有B选项三角形符合，与所给图形的三角形相似．
    故选B．
    点评：本题考查了相似三角形的判定，勾股定理的应用，熟练掌握网格结构，观察出所给图形的直角三角形的特点是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，在5×5的正方形网格中，点A、B、C、E、F都在小正方形的顶点上，试在该网格中找点D，连接DE、DF，使得△DEF与△ACB相似，且点E与点C对应，点F与点B对应．
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网“构造法”是一种重要方法，它没有固定的模式．要想用好它，需要有敏锐的观察、丰富的想象、灵活的构思．应用构造法解题的关键有二：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行组合．
    例：在△ABC中，AB、BC、AC三边长分别是
    		5
    、
    		10
    、
    		13
    ，求这个三角形的面积．
    小辉在解这道题时，画一个正方形网格（每个正方形的边长为1），再在网格中画出格点（即的顶点都在小正方形的顶点处），如图1所示，这样不需要求的高，借助网格就能计算出它的面积．图中的面积，可以看成是一个的正方形的面积减去三个小三角形的面积：S△ABC=3×3-
    1
    2
    ×3×1-
    1
    2
    ×2×1-
    1
    2
    ×3×2=
    7
    2

    思维拓展：已知△ABC的边长分别为
    		5a
    、2
    		2a
    、
    		17a
    (a＞0)    ，请在下图所示的正方形网格中（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

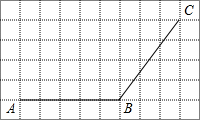    如图所示给出的是10×6的网格，网格中的每个小正方形的边长均为1，点A、B、C在小正方形的顶点上．
    （1）在图中画线段AD（点D在小正方形的顶点上），使AD∥BC，连接CD．
    （2）直接写出四边形ABCD的周长为
    20
    20
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在小正方形的网格中，下列四个选项中的三角形，与如图所示的三角形相似的是（　　）

    查看答案和解析>>

    同步练习册答案