
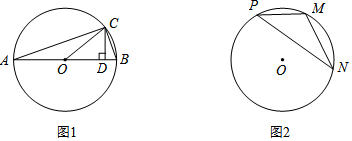
分析 (1)如图1中,⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα=$\frac{BC}{AB}$=$\frac{1}{3}$,可设BC=x,则AB=3x.利用面积法求出CD,在Rt△COD中,根据sin2α=$\frac{CD}{OC}$,计算即可.
(2)如图2中,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR⊥NO于点R.首先证明∠MON=2∠Q=2β,
在Rt△QMN中,由sinβ=$\frac{MN}{NQ}=\frac{3}{5}$,设MN=3k,则NQ=5k,易得OM=$\frac{1}{2}$NQ=$\frac{5}{2}k$,可得MQ=$\sqrt{Q{N^2}-M{N^2}}=4k$,由$\frac{1}{2}$•MN•MQ=$\frac{1}{2}$•NQ•MR,求出在Rt△MRO中,根据sin2β=sin∠MON=$\frac{MR}{OM}$,计算即可.
解答 解:(1)如图1中,⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα=$\frac{BC}{AB}$=$\frac{1}{3}$,可设BC=x,则AB=3x.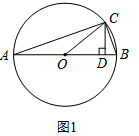
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{(3x)^{2}-{x}^{2}}$=2$\sqrt{2}$x,
∵$\frac{1}{2}$•AC•BC=$\frac{1}{2}$•AB•CD,
∴CD=$\frac{2\sqrt{2}}{3}$x,
∵OA=OC,
∴∠OAC=∠OCA=α,
∴∠COB=2α,
∴sin2α=$\frac{CD}{OC}$=$\frac{{4\sqrt{2}}}{9}$.
(2)如图2中,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR⊥NO于点R.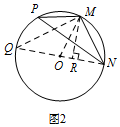
在⊙O中,∠NMQ=90°,
∵∠Q=∠P=β,∴∠MON=2∠Q=2β,
在Rt△QMN中,∵sinβ=$\frac{MN}{NQ}=\frac{3}{5}$,
∴设MN=3k,则NQ=5k,易得OM=$\frac{1}{2}$NQ=$\frac{5}{2}k$,
∴MQ=$\sqrt{Q{N^2}-M{N^2}}=4k$,
∵${S_{△NMQ}}=\frac{1}{2}MN•MQ=\frac{1}{2}NQ•MR$,
∴3k•4k=5k•MR
∴MR=$\frac{12}{5}k$,
在Rt△MRO中,sin2β=sin∠MON=$\frac{MR}{OM}=\frac{{\frac{12}{5}k}}{{\frac{5k}{2}}}=\frac{24}{25}$.
点评 本题考查圆综合题、锐角三角函数,等腰三角形的性质,圆周角定理、勾股定理等知识,解题的关键是学会添加常用辅助线,本题的突破点是找到两倍角,属于中考压轴题.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
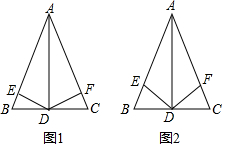 (1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.
(1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
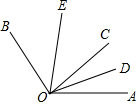 如图,∠AOB=120°,射线OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )
如图,∠AOB=120°,射线OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )| A. | ∠DOE的度数不能确定 | B. | ∠AOD=∠EOC | ||
| C. | ∠AOD+∠BOE=60° | D. | ∠BOE=2∠COD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
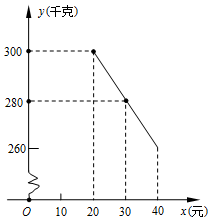 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
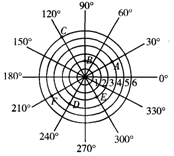 如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( )
如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( )| A. | A(4,30°) | B. | B(2,90°) | C. | C(6,120°) | D. | D(3,240°) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 86×102 | B. | 8.6×103 | C. | 86×103 | D. | 0.86×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
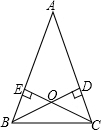 如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.
如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com