
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论:![]() ;
;![]() >0;(3)若点
>0;(3)若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.
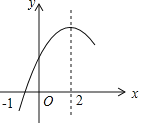
 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
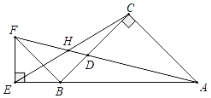
【题目】如图,点A、B、E在同一直线上,∠FEB=∠ACB=90°,AC=BC,EB=EF,连AF,CE交于点H,AF、CB交于点D,若tan∠CAD=![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,乙品牌消毒剂每瓶的价格比甲品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲品牌消毒剂的数量与用400元购买乙品牌消毒剂的数量相同.
(1)求甲、乙两种品牌消毒剂每瓶的价格各是多少元?
(2)若该小区从超市一次性购买甲、乙两种品牌的消毒剂共40瓶,且总费用为1400元,求购买了多少瓶乙品牌消毒剂?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,对于已知一次函数y1=ax+b,y2=cx+d(其中a,b,c,d为常数,且ac<0),定义一个新函数y=![]() ,称y是y1与y2的算术中项,y是x的算术中项函数.
,称y是y1与y2的算术中项,y是x的算术中项函数.
(1)如:一次函数y1=![]() x﹣4,y2=﹣
x﹣4,y2=﹣![]() x+6,y是x的算术中项函数,即y=
x+6,y是x的算术中项函数,即y= .
.
①自变量x的取值范围是 ,当x= 时,y有最大值;
②根据函数研究的途径与方法,请填写下表,并在图1中描点、连线,画出此函数的大致图象;
x | 8 | 9 | 10 | 12 | 13 | 14 | 16 | 17 | 18 |
y | 0 | 1.2 | 1.6 |
| 2.04 | 2 |
| 1.2 | 0 |

③请写出一条此函数可能有的性质 ;
(2)如图2,已知一次函数y1=![]() x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y=
x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y= .
.
①判断:点A、C、E是否在此算术中项函数的图象上;
②在平面直角坐标系中是否存在一点,到此算术中项函数图象上所有点的距离相等,如果存在,请求出这个点;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 为
为![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() 并延长
并延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
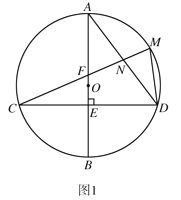
(1)如图1,连接![]() .求证:
.求证:![]() ;
;
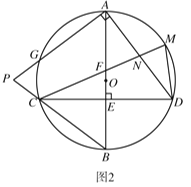
(2)如图2,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() 求证:
求证:![]() .
.
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,在△ABC中,∠BCA=90°,AC=kBC,点D,E分别在边BC,AC上,且AE=kCD,作线段DF⊥DE,且DE=kDF,连接EF交AB于点G.
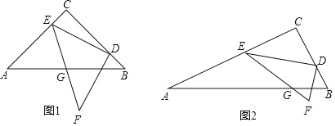
(1)如图1,当k=1时,求证:①∠CED=∠BDF,②AG=GB;
(2)如图2,当k≠1时,猜想![]() 的值,并说明理由;
的值,并说明理由;
(3)当k=2,AE=4BD时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
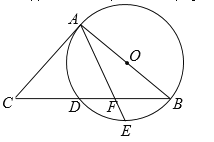
【题目】如图,AB是⊙O的直径, BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB =2∠EAB.
的中点,连接AE交BC于点F,∠ACB =2∠EAB.
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)若![]() ,
,![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
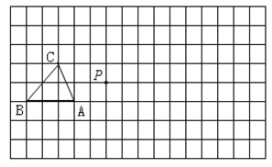
【题目】在下面的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处) .
(1)作出△ABC的中心对称图形△![]() ,A点为对称中心;
,A点为对称中心;
(2)作出△ABC关于点P的位似△A'B'C',且位似比为1:2;
(3)在图中画出以A、B、C为顶点的平行四边形的第四个顶点D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB的半径OA=4,圆心角∠AOB=90°,点C是弧AB上异于A、B的一点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,过点C作弧AB所在圆的切线CG交OA的延长线于点G.
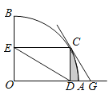
(1)求证:∠CGO=∠CDE;
(2)若∠CGD=60°,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com