
【题目】如图,直线y=﹣ ![]() x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.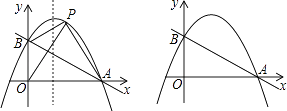
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的 ![]() 倍.
倍.
①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
【答案】
(1)
解:∵直线y=﹣ ![]() x+1与x轴交于点A,与y轴交于点B,
x+1与x轴交于点A,与y轴交于点B,
∴A(2,0),B(0,1),
∵抛物线y=﹣x2+bx+c经过A、B两点,
∴ ![]() ,
,
∴ ![]()
∴抛物线解析式为y=﹣x2+ ![]() x+1
x+1
(2)
解:①由(1)知,A(2,0),B(0,1),
∴OA=2,OB=1,
由(1)知,抛物线解析式为y=﹣x2+ ![]() x+1,
x+1,
∵点P是第一象限抛物线上的一点,
∴设P(a,﹣a2+ ![]() a+1),((a>0,﹣a2+
a+1),((a>0,﹣a2+ ![]() a+1>0),
a+1>0),
∴S△POA= ![]() OA×Py=
OA×Py= ![]() ×2×(﹣a2+
×2×(﹣a2+ ![]() a+1)=﹣a2+
a+1)=﹣a2+ ![]() a+1
a+1
S△POB= ![]() OB×Px=
OB×Px= ![]() ×1×a=
×1×a= ![]() a
a
∵△POA的面积是△POB面积的 ![]() 倍.
倍.
∴﹣a2+ ![]() a+1=
a+1= ![]() ×
× ![]() a,
a,
∴a= ![]() 或a=﹣
或a=﹣ ![]() (舍)
(舍)
∴P( ![]() ,1);
,1);
②如图1,

由(1)知,抛物线解析式为y=﹣x2+ ![]() x+1,
x+1,
∴抛物线的对称轴为x= ![]() ,抛物线与x轴的另一交点为C(﹣
,抛物线与x轴的另一交点为C(﹣ ![]() ,0),
,0),
∵点A与点C关于对称轴对称,
∴QP+QA的最小值就是PC= ![]() ;
;
(3)
①当OB为平行四边形的边时,MN=OB=1,MN∥OB,
∵点N在直线AB上,
∴设M(m,﹣ ![]() m+1),
m+1),
∴N(m,﹣m2+ ![]() m+1),
m+1),
∴MN=|﹣m2+ ![]() m+1﹣(﹣
m+1﹣(﹣ ![]() m+1)|=|m2﹣2m|=1,
m+1)|=|m2﹣2m|=1,
Ⅰ、m2﹣2m=1,
解得,m=1± ![]() ,
,
∴M(1+ ![]() ,
, ![]() (1﹣
(1﹣ ![]() ))或M(1﹣
))或M(1﹣ ![]() ,
, ![]() (1+
(1+ ![]() ))
))
Ⅱ、m2﹣2m=﹣1,
解得,m=1,
∴M(1, ![]() );
);
②当OB为对角线时,OB与MN互相平分,交点为H,
∴OH=BH,MH=NH,
∵B(0,1),O(0,0),
∴H(0, ![]() ),
),
设M(n,﹣ ![]() n+1),N(d,﹣d2+
n+1),N(d,﹣d2+ ![]() d+1)
d+1)
∴  ,
,
∴ ![]() 或
或 ![]() ,
,
∴M(﹣(1+ ![]() ),
), ![]() (3+
(3+ ![]() ))或M(﹣(1﹣
))或M(﹣(1﹣ ![]() ),
), ![]() (3﹣
(3﹣ ![]() ));
));
即:满足条件的点M的坐标(1+ ![]() ,
, ![]() (1﹣
(1﹣ ![]() ))或(1﹣
))或(1﹣ ![]() ,﹣
,﹣ ![]() (1+
(1+ ![]() ))或(1,
))或(1, ![]() )或M(﹣(1+
)或M(﹣(1+ ![]() ),
), ![]() (3+
(3+ ![]() ))或M(﹣(1﹣
))或M(﹣(1﹣ ![]() ),
), ![]() (3﹣
(3﹣ ![]() ))
))
【解析】(1)先确定出点A,B坐标,再用待定系数法求出抛物线解析式;(2)设出点P的坐标,①用△POA的面积是△POB面积的 ![]() 倍,建立方程求解即可;②利用对称性找到最小线段,用两点间距离公式求解即可;(3)分OB为边和为对角线两种情况进行求解,①当OB为平行四边形的边时,用MN∥OB,表示和用MN=OB,建立方程求解;
倍,建立方程求解即可;②利用对称性找到最小线段,用两点间距离公式求解即可;(3)分OB为边和为对角线两种情况进行求解,①当OB为平行四边形的边时,用MN∥OB,表示和用MN=OB,建立方程求解;
②当OB为对角线时,OB与MN互相平分,交点为H,设出M,N坐标用OH=BH,MH=NH,建立方程组求解即可.


科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方正确的是( )
A.方程x2﹣6x﹣5=0,可化为(x﹣3)2=4
B.方程y2﹣2y﹣2015=0,可化为(y﹣1)2=2015
C.方程a2+8a+9=0,可化为(a+4)2=25
D.方程2x2﹣6x﹣7=0,可化为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.

(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将半径为3cm,圆心角为60°的扇形纸片.AOB在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长 cm(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠BAC=60°,AD=AE,BE、CD交于点F,且∠DFE=120°.在BE的延长线上截取ET=DC,连接AT.
(1)求证:∠ADC=∠AET;
(2)求证:AT=AC;
(3)设BC边上的中线AP与BE交于Q.求证:∠QAB=∠QBA.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com