
����Ŀ����������һ�����dz߷��ڱ߳�Ϊ1��������ABCD�ϣ���ʹ����ֱ�Ƕ���P�ڶԽ���AC�ϻ�����ֱ�ǵ�һ��ʼ�վ�����B����һ��������DC�ཻ�ڵ�Q����A��P�����ľ���Ϊx��
̽����
��1������Q�ڱ�CD��ʱ���߶�PQ���߶�PB֮���������Ĵ�С��ϵ����֤����۲쵽�Ľ��ۣ�
��2������Q�ڱ�CD��ʱ�����ı���PBCQ�����Ϊy����y��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ����3������P���߶�AC�ϻ���ʱ����PCQ�Ƿ��ܳ�Ϊ���������Σ�������ܣ�ָ��������ʹ��PCQ��Ϊ���������εĵ�Q��λ�ã��������Ӧx��ֵ����������ܣ���˵�����ɣ�
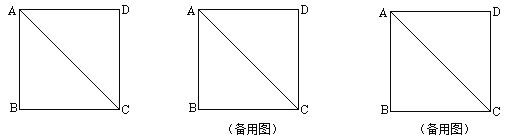
���𰸡���1����PQ=PB��֤�����̼���������2����y=![]() ��0��x��
��0��x��![]() ������3����x��0��1.
������3����x��0��1.
�����������������(1)������P��MN��BC���ֱ�AB��CD�ڵ�M��N�����ı���AMND���ı���BCNM���Ǿ��Σ���AMP����CNP���ǵ��������Σ��ó�NP=NC=MB���Ӷ�֤����QNP�ա�PMB���Ӷ��ó��𰸣�(2)����AP=x����M��MP��NQ��DN��![]() x��BM��PN��CN��1��
x��BM��PN��CN��1��![]() x����������ó���PBC����PCQ�������Ȼ��ó�y��x�ĺ�����ϵʽ��(3)���������������������ۣ���������Q�ڱ�DC�ϣ�������Q�ڱ�DC���ӳ����ϣ�������Q��C���غ�.
x����������ó���PBC����PCQ�������Ȼ��ó�y��x�ĺ�����ϵʽ��(3)���������������������ۣ���������Q�ڱ�DC�ϣ�������Q�ڱ�DC���ӳ����ϣ�������Q��C���غ�.
���������(1)������P��MN��BC���ֱ�AB��CD�ڵ�M��N�����ı���AMND���ı���BCNM���Ǿ��Σ�
��AMP����CNP���ǵ��������Σ���ͼ1������NP��NC��MB��
�ߡ�BPQ��90����QPN����BPM��90��������BPM����PBM��90����QPN����PBM��
���ߡ�QNP����PMB��90����QNP�ա�PMB��ASA������PQ��PB��
(2)����(1)֪��QNP�ա�PMB����NQ��MP��
��AP��x����AM��MP��NQ��DN��![]() x��BM��PN��CN��1��
x��BM��PN��CN��1��![]() x ��CQ��CD��DQ��1��2��
x ��CQ��CD��DQ��1��2��![]() x��1��
x��1��![]() x
x
��S��PBC��BCBM����1��(1��![]() x)��
x)��![]() ��
��![]() x��
x��
S��PCQ��CQPN����(1��![]() x)(1��
x)(1��![]() x)��
x)��![]() ��
��
��S�ı���PBCQ��S��PBC��S��PCQ��![]() �� ��y��
�� ��y��![]() ��0��x��
��0��x��![]() ����
����
(3)����PCQ���ܳ�Ϊ���������Σ�
������Q�ڱ�DC�ϣ���![]() �ã�
�ã�![]()
���x1��0��x2��![]() (��ȥ)��
(��ȥ)��
������Q�ڱ�DC���ӳ����ϣ���ͼ2������PC��CQ�ã�![]() ��x��
��x��![]() x��1��
x��1��
���x��1��
������Q��C���غϣ���PCQ�����ڣ�
����������x��0��1ʱ����PCQΪ����������
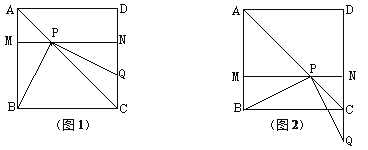



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
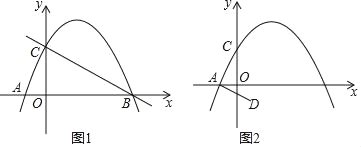
����Ŀ����֪��������y=��![]() x2+bx+c��x���ڵ�A����1��0���͵�B����y���ڵ�C��0��2��
x2+bx+c��x���ڵ�A����1��0���͵�B����y���ڵ�C��0��2��
��1���������ߵı���ʽ��
��2����PΪ��һ������������һ�㣬�Ƿ����ʹ��PBC������ĵ�P���������ڣ���˵�����ɣ������ڣ������P�����ꣻ
��3����D����Ϊ��1����1��������AD�����߶�AD��ƽ����ijһ����ת180�ȵ��߶�MN����M��N�ֱ����A��D��Ӧ����ʹ��M��N�����������ϣ����M��N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
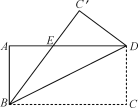
����Ŀ����ͼ��������ABCD����ֱ��BD�۵���ʹ��C����C������BC����AD�ڵ�E��CD��6��BC��8����DE�ij���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
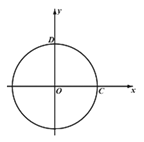
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=��![]() ��b(b��0,bΪ����)��ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B���뾶Ϊ4�ġ�O��x�������ύ�ڵ�C����y���������ཻ�ڵ�D.
��b(b��0,bΪ����)��ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B���뾶Ϊ4�ġ�O��x�������ύ�ڵ�C����y���������ཻ�ڵ�D.
(1)��ֱ��AB���O�����ڻ�CD��һ�㣬��b��ֵ��
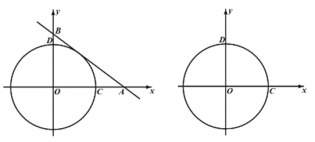
(2)��ֱ��AB���O����������F��G.
��bΪ��ֵʱ����O������ֻ��3���㵽ֱ��AB�ľ���Ϊ2���������ʱֱ�߱���O���ص���FG�ij���
���Ƿ����������b��ʹ�á�GOF=90�㣿�����������b��ֵ������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
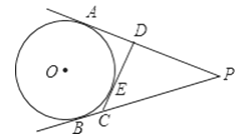
����Ŀ����ͼ��PA��PB�С�O��A��B���㣬CD�С�O�ڵ�E���ֱ�PA��PB�ڵ�C��D����PA��PB�ij��ǹ���x��һԪ���η���x2��mx+m��1=0�������������PCD���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���![]() �ı�
�ı�![]() ��
��![]() ��
��![]() ��
��![]() Ϊб�߷ֱ������������ֱ�������Σ�ֱ�Ƕ���ֱ�Ϊ
Ϊб�߷ֱ������������ֱ�������Σ�ֱ�Ƕ���ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
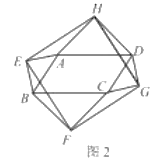
��![]() ��˳���������ĸ��㣬���ı���
��˳���������ĸ��㣬���ı���![]() ��
��
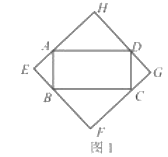
��1����ͼ1�����ı���![]() Ϊ����ʱ�����ж��ı���
Ϊ����ʱ�����ж��ı���![]() ����״����Ҫ��֤������
����״����Ҫ��֤������
��2����ͼ2�����ı���![]() Ϊһ��ƽ���ı���ʱ����
Ϊһ��ƽ���ı���ʱ����![]()
�����ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��д�������̣�
��д�������̣�
����֤��![]() �����ж��ı���
�����ж��ı���![]() ��ʲô�ı��Σ���˵�����ɣ�
��ʲô�ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
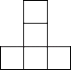
����Ŀ�������ɸ�С��������һ�������壬ʹ�������濴������濴������ͼ��ͬһ��ͼ��ͨ��ʵ�ʲ���������ͬѧ�����ۣ�����������⣺
��1������Ҫ��С������ĸ����Ƕ��٣������ҳ����֣�
��2����������������ٺ�����������ļ���������濴����ͼ������С��������ע���ڸ�λ����С������ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ��������֮��ͬ��С�ij��˵��⣬�������ĸ���������AB=BC���ڡ�ABC=90������AC=BD����AC��BD��ѡ������Ϊ����������ʹABCDΪ�����Σ���ͼ����������������ѡ��������Ϊ���д�����ǣ� ��

A.�٢�B.�ڢ�C.�٢�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���εı߳���һ���Խ��ߵij���Ϊ2 cm�������ε����Ϊ( )
A. 3cm2 B. 4 cm2 C. ![]() cm2 D. 2
cm2 D. 2![]() cm2
cm2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com