
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF,且CF=EF.
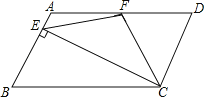
(1)若∠CFD=55°,求∠BCD的度数;
(2)求证:∠EFC=2∠CFD;
(3)求证:CE⊥AB.
【答案】(1)110°;(2)见解析;(3)见解析
【解析】
试题分析:(1)根据平行四边形的性质得出AD∥BC,根据平行线的性质得出∠BCF=∠CFD=55°,求出DF=DC,根据等腰三角形的性质得出∠DCF=∠CFD=55°,即可求出答案;
(2)延长EF和CD交于M,根据平行四边形的性质得出AB∥CD,根据平行线的性质得出∠A=∠FDM,证△EAF≌△MDF,推出EF=MF,求出CF=MF,求出∠M=∠FCD=∠CFD,根据三角形的外角性质求出即可;
(3)求出∠ECD=90°,根据平行线的性质得出∠BEC=∠ECD,即可得出答案.
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠CFD=55°,
∴∠BCF=∠CFD=55°,
∵在ABCD中,AD=2AB,
∴AD=2DC,
∵F为AD的中点,
∴AF=DF,AD=2DF,
∴DF=DC,
∴∠DCF=∠CFD=55°,
∴∠BCD=∠BCF+∠DCF=55°+55°=110°;
(2)证明:延长EF和CD交于M,
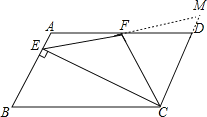
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠FDM,
在△EAF和△MDF中,
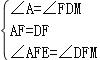 ,
,
∴△EAF≌△MDF(ASA),
∴EF=MF,
∵EF=CF,
∴CF=MF,
∴∠FCD=∠M,
∵由(1)知:∠DFC=∠FCD,
∴∠M=∠FCD=∠CFD,
∵∠EFC=∠M+∠FCD=2∠CFD;
(3)解:∵EF=FM=CF,
∴∠ECM=90°,
∵AB∥CD,
∴∠BEC=∠ECM=90°,
∴CE⊥AB.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】用配方法解方程x2-2x-2=0,下列配方正确的是( )
A. (x-1)2=2 B. (x-1)2=3 C. (x-2)2=3 D. (x-2)2=6
查看答案和解析>>
科目:初中数学 来源: 题型:
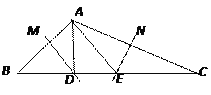
【题目】如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形的餐桌可以坐6个人,按照下图的方式摆放餐桌和椅子:

(1)观察表中数据规律填表:
餐桌张数 | 1 | 2 | 3 | 4 | …n |
可坐人数 | 6 | 8 | 10 |
(2)一家酒楼,按上图的方式拼桌,要使拼成的一张大餐桌刚好能坐160人,请问需几张餐桌拼成一张大餐桌?
(3)若酒店有240人来就餐,哪种拼桌的方式更好?最少要用多少张餐桌?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=36°,DE是AB的垂直平分线,DE交AB于点D,交AC于点E,连接BE.下列结论①BE平分∠ABC;②AE=BE=BC;③△BEC周长等于AC+BC;④E点是AC的中点.其中正确的结论有 (填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【现场学习】
定义:我们把绝对值符号内含有未知数的方程叫做“含有绝对值的方程”.
如:|x|=2,|2x﹣1|=3,|![]() |﹣x=1,…都是含有绝对值的方程.
|﹣x=1,…都是含有绝对值的方程.
怎样求含有绝对值的方程的解呢?基本思路是:含有绝对值的方程→不含有绝对值的方程.
我们知道,根据绝对值的意义,由|x|=2,可得x=2或x=﹣2.
[例]解方程:|2x﹣1|=3.
我们只要把2x﹣1看成一个整体就可以根据绝对值的意义进一步解决问题.
解:根据绝对值的意义,得2x﹣1=3或2x﹣1= .
解这两个一元一次方程,得x=2或x=﹣1.
检验:
(1)当x=2时,
原方程的左边=|2x﹣1|=|2×2﹣1|=3,
原方程的右边=3,
∵左边=右边
∴x=2是原方程的解.
(2)当x=﹣1时,
原方程的左边=|2x﹣1|=|2×(﹣1)﹣1|=3,
原方程的右边=3,
∵左边=右边
∴x=﹣1是原方程的解.
综合(1)(2)可知,原方程的解是:x=2,x=﹣1.
【解决问题】
解方程:|![]() |﹣x=1.
|﹣x=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
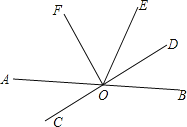
【题目】如图,直线AB与CD相交于点O,OD平分∠BOE,∠FOD=90°,问OF是∠AOE的平分线吗?请你补充完整小红的解答过程.
探究:
(1)当∠BOE=70°时,
∠BOD=∠DOE=![]() ,
,
∠EOF=90°﹣∠DOE= °,
而∠AOF+∠FOD+∠BOD=180°,
所以∠AOF+∠BOD=180°﹣∠FOD=90°,
所以∠AOF=90°﹣∠BOD= °,
所以∠EOF=∠AOF,OF是∠AOE的平分线.
(2)参考上面(1)的解答过程,请你证明,当∠BOE为任意角度时,OF是∠AOE的平分线.
(3)直接写出与∠AOF互余的所有角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com