
����Ŀ��Ϊ���¹���Ʒ�֣�ij���ƻ��¹���![]() ��
��![]() ����Ʒ�ֵĹ�������ֲ���������ƻ����������ֹ����繲45�ã�����
����Ʒ�ֵĹ�������ֲ���������ƻ����������ֹ����繲45�ã�����![]() ����ĵ���Ϊ8Ԫ/�ã�����
����ĵ���Ϊ8Ԫ/�ã�����![]() �����������
�����������![]() ��Ԫ���빺������
��Ԫ���빺������![]() ���ã�֮�������ͼ��ʾ�ĺ�����ϵ��
���ã�֮�������ͼ��ʾ�ĺ�����ϵ��
��1����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�����ڹ���ƻ��У�![]() ���������������35�ã���������
���������������35�ã���������![]() ����������һ�룬����ƹ�����ʹ�ܷ�����ͣ��������ͷ��ã�
����������һ�룬����ƹ�����ʹ�ܷ�����ͣ��������ͷ��ã�

���𰸡���1��![]() ����2��B���������35�ã�������ͣ�330Ԫ
����2��B���������35�ã�������ͣ�330Ԫ
��������
(1)���ݺ���ͼ���е����ݿ������y��x�ĺ�����ϵʽ��
(2)����(1)�еĺ�����ϵʽ�����⣬������÷��õ���Сֵ������Ӧ�ĵĹ�����
�⣺��1����0��x��20ʱ����y��x�ĺ�����ϵʽΪ��y��k1x��
�ѣ�20��160�����룬�ã�
20k��b��160��
���k��8��
��ʱy��x�ĺ�����ϵʽΪy��8x��
��20��x��45ʱ���ѣ�20��160������40��280������y��k2x��b�У���
 ���
���![]()
��ʱy��x�ĺ�����ϵʽΪy��6x��40��
���Ͽ�֪��y��x�ĺ�����ϵʽΪ![]()
��2�����蹺��B������x�ã�B���������������35�ã���������A����������һ�룬
��
���15��x��35��
���ܷ���ΪWԪ��
��15x20ʱ��
W=8(45x)+8x=360��
��20<x35ʱ��
��W��6x��40��8��45��x������2x��400��
��k����2��
��y��x�����������
�൱x=35ʱ��Wȡ����Сֵ����ʱW=330��
�൱x��35ʱ��W�ܷ�����ͣ�W�����330��Ԫ����
�𣺵�����B������35��ʱ�ܷ�����ͣ���ͷ�����330Ԫ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=kx+b��x���ڵ�A����y���ڵ�B��ֱ��y=2x��4��x���ڵ�D����ֱ��AB�ཻ�ڵ�C��3��2����
��1������ͼ��д������x�IJ���ʽ2x��4��kx+b�Ľ⼯��
��2������A������Ϊ��5��0������ֱ��AB�Ľ���ʽ��
��3���ڣ�2���������£����ı���BODC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
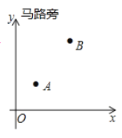
����Ŀ��Ҫ����·����һ����������Ͷ�ŵ㣬��![]() ���ҹ�˾�ṩ����Ͷ�ŵ�Ӧ����ʲô�ط�������ʹ��
���ҹ�˾�ṩ����Ͷ�ŵ�Ӧ����ʲô�ط�������ʹ��![]() �����ľ���֮����̣�С������ʵ�����������·Ϊ
�����ľ���֮����̣�С������ʵ�����������·Ϊ![]() �Ὠ������ͼ��ʾ��ƽ��ֱ������ϵ��
�Ὠ������ͼ��ʾ��ƽ��ֱ������ϵ��![]() �������Ϊ
�������Ϊ![]() ��
��![]() �������Ϊ
�������Ϊ![]() �����
�����![]() ���㵽Ͷ�ŵ����֮�͵���Сֵ��__________��Ͷ�ŵ��������__________��
���㵽Ͷ�ŵ����֮�͵���Сֵ��__________��Ͷ�ŵ��������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
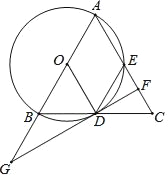
����Ŀ����ͼ����ABC�У�AB=AC����ABΪֱ���ġ�O��BC��AC��D��E���㣬����D����O�����ߣ���AC�ڵ�F����AB���ӳ����ڵ�G��
��1����֤��EF=CF��
��2����cos��ABC=![]() ��AB=10�����߶�AF�ij���
��AB=10�����߶�AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣺��y��z��2+��x��y��2+��z��x��2=��y+z��2x��2+��z+x��2y��2+��x+y��2z��2��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ������Բ
������Բ![]() ����߷ֱ������ڵ�
����߷ֱ������ڵ�![]() ��
��![]() ��
��![]() ����ô��������������ǣ� ��
����ô��������������ǣ� ��
A. ��![]() ��
��![]() ��������ƽ���ߵĽ��� B. ��
��������ƽ���ߵĽ��� B. ��![]() ��
��![]() ���������ߵĽ���
���������ߵĽ���
C. ��![]() ��
��![]() �������ߵĴ�ֱƽ���ߵĽ��� D.
�������ߵĴ�ֱƽ���ߵĽ��� D. ![]() һ�������������
һ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
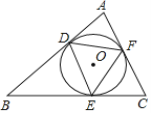
����Ŀ����ͼ����һ��ʯ���ŵ��Ź�����![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��һ��Բ����
Ϊ�뾶��һ��Բ����

![]() ����ȷ����
����ȷ����![]() ���е㣻��Ҫ���ó߹���ͼ��������ͼ�ۼ�����д������֤����
���е㣻��Ҫ���ó߹���ͼ��������ͼ�ۼ�����д������֤����
![]() �����֪ʯ���ŵ��Ź��Ŀ�ȣ��������Ե��ҳ���Ϊ
�����֪ʯ���ŵ��Ź��Ŀ�ȣ��������Ե��ҳ���Ϊ![]() �ף����ߣ��������е㵽�ҵľ��룩Ϊ
�ף����ߣ��������е㵽�ҵľ��룩Ϊ![]() �ף����Ź�����Բ�İ뾶��
�ף����Ź�����Բ�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
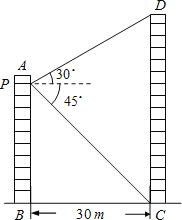
����Ŀ����ͼ��ʾ������������AB��CD��ˮƽ����Ϊ30m������ͬѧס�ڽ�����AB��10¥P�ң����۲⽨����CD¥�Ķ���D��������Ϊ30������õײ�C���ĸ���Ϊ45����������CD�ĸ߶ȣ���![]() ȡ1.73�����������������
ȡ1.73�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�������������ֱ�ΪA��1��1����B��4��2����C��3��4����
��1���뻭����ABC����y��ĶԳ�ͼ�Ρ�A1B1C1��
��2����y��������һ��P��ʹ��PAC���ܳ���С����ֱ��д��P�����꣮

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com